今回の記事では虫食い算について取り扱っていきます。虫食い算は式の筆算を基準とした問題で,単純な四則演算の応用で解くことができるものの,受験算数となると難しい問題もたくさん出題されやすいのもこの虫食い算という単元です。そのため本記事を読んで対策していきましょう。
虫食い算とは…?
まずは解説本編に移っていく前に,虫食い算とはどのような問題を指すのかということを確認していきましょう。虫食い算とは筆算をいじって作り出された問題のことを指します。普通筆算は2つなり3つなりの数字を縦に並べて,それを位ごとに計算していきますね。その計算過程の一部が□で分からなくなっているものがこの虫食い算であり,虫に食われたような様子から虫食い算と名付けられました。そして虫食い算ではどうにかしてその抜けた□の中身を考えて当てる,ということが求められます。具体的には次のような問題を指します。似たように筆算と□が組み合わさったような問題はすべて虫食い算だと思ってしまっていいでしょう。
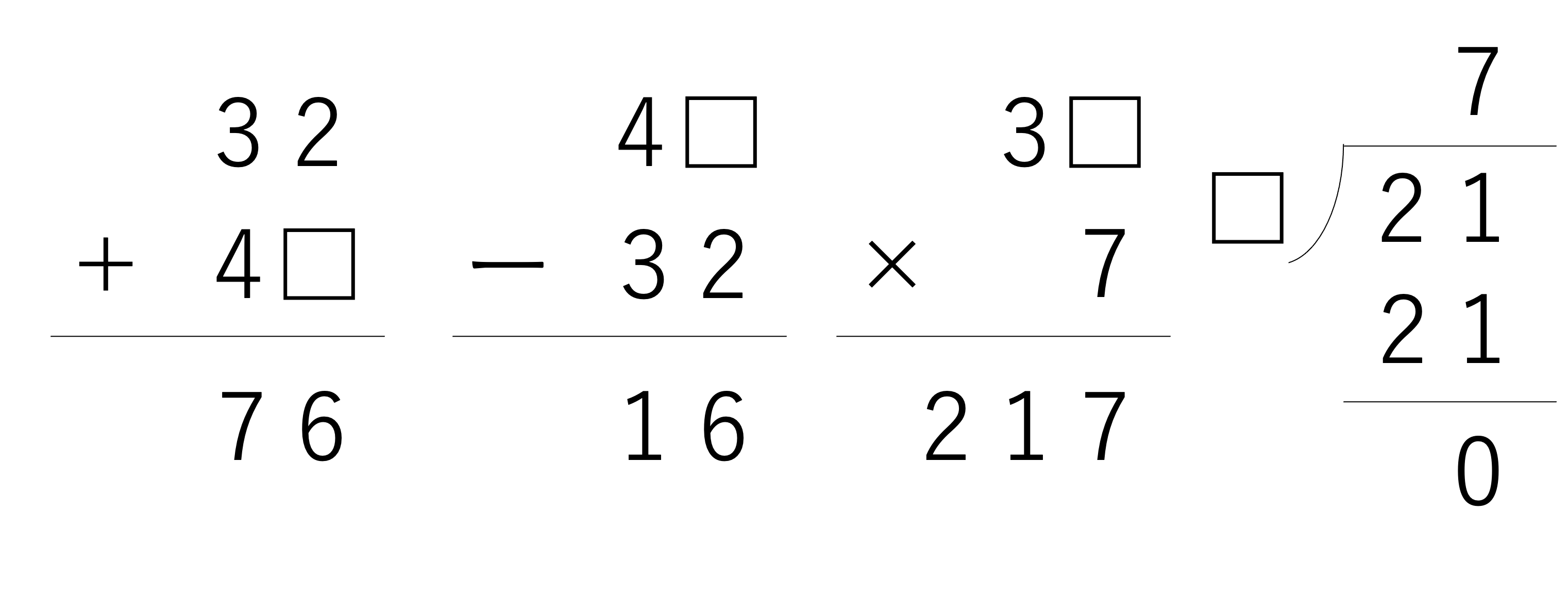
これらの問題のように,筆算をベースとしている虫食い算は+・―・×・÷のすべての計算に関して作成することができます。また登場する数字の桁数や□の数も難易度によって異なりますが,今回の記事では基本編として2けた×2けたの計算を中心として,また□の数も少なめのものを取り扱いながら解説していきます。
足し算の虫食い算
まずは足し算の虫食い算について考えていきましょう。わかりやすい例として,先ほど載せた32+4□=76というものを取り扱っていきます。改めて掲載しておきますので,どうやって解けばいいのか・答えは何になるのかを考えてみましょう。
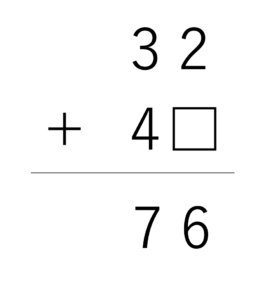
さて虫食い算の解き方ですが,すべての四則演算,とくに足し算と引き算に共通して重要なのがそれぞれの位ごとに式を組み立てていくというステップです。虫食い算とは筆算を発展させた問題ですので,筆算の解き方を応用していけば基本的には解くことができます。そして筆算を解く上で意識するポイントはそれぞれの位ごとに順番に計算していくということでした。例えば今回の問題だと,筆算は次のような手順で行われますよね。
2+□=6
3+4=7
このような位ごと式を作っていくことで,よりわかりやすく□の関係を理解することができます。今回の問題だと,2と□を足した値が答えの一の位である6に相当するということが分かるため,逆算を応用して考えると□には4が入ることがわかり,したがって答えは4となります。
A.4
なお問題によっては筆算の繰り上がり・繰り下がりが登場することもあります。例えば一の位が6と7の2けたの数字を筆算で足し算すると13となりますが,このとき13の10の部分は隣の位でカウントされるため,位ごとの式を立てると6+7=3という見た目になりますよね。このような繰り上がりの式が登場してしまった場合,位ごとの式がうまく成立しない場合が発生します。そのようなときは焦らずに,末尾の位を一致させるようにして計算を進めていけば問題なく解答を得ることができます。
先ほどの6+7の計算を応用して,例題として36+4□=83という問題を用意しました。このとき一の位では6+□=3という式が出来上がりますが,足し算の答えが足す前の数より小さくなっていることから正しい式にはなっていないと言えます。そのような場合は末尾の3に注目し,足したら末尾が◯3という形になる数字を探せばいいですね。そして今回だと7が当てはまるので,□に入る答えは7となります。このとき一の位の計算では13という値が導かれますが,いま十の位に1繰り上がることを考えると,3+4+1=8とこちらの計算も正しく成立するようになりますよね。このように末尾に注目すれば繰り上がり,また繰り下がりの問題も難なく答えることができます。

引き算の虫食い算
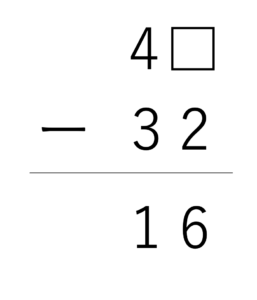
続いては引き算の虫食い算の解き方を解説していきましょう。今回も先ほど載せた4□-32の計算を例として取り上げながら解説していきます。改めて下に問題を提示しておきますので,答えがどうなるか考えてみてください。
先ほど足し算の虫食い算において,位ごとの式を立てると□の中身を計算することができると説明しましたね。実は引き算の虫食い算でも同じようにして問題の答えを得ることができるのです。足し算のときの要領で考えると,今回の問題では一の位と十の位に関して次のような式を立てることができますね。
□-2=6
4-3=1
このときの上の式について考えることで,□の値を求めることができますね。逆算の要領でこの式は6-2=□と書き換えられるので,□には6から2を引いた数,すなわち4が当てはまることが分かります。したがって答えは4となるわけです。
A.4
以上のように足し算のケースの応用で引き算の虫食い算は解くことができるわけですが,繰り下がりが発生する場合についても足し算の繰り上がりと同様の手法で計算することができます。例として下のような問題を使いながら繰り下がりが発生する問題の解き方を確認していきましょう。
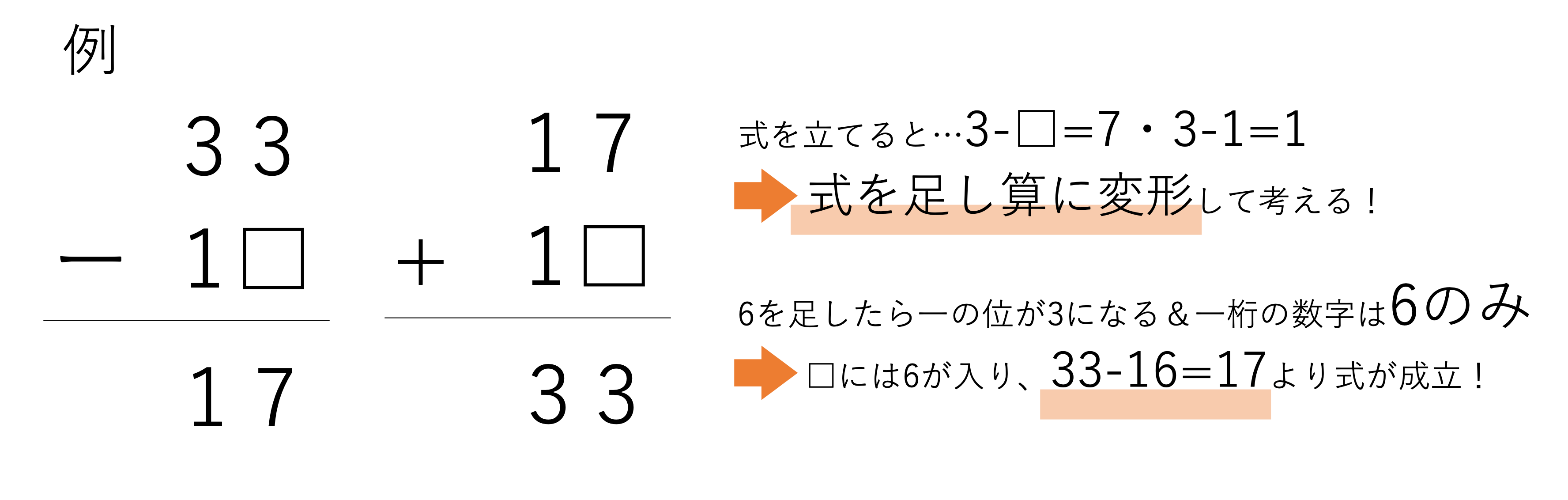
この33-1□=17という問題をみながら繰り下がりが発生するときの攻略法を抑えていきましょう。上の筆算において位ごとの式を立てると,一の位で3-□=7という不自然な式が出来上がってしまいますよね。というのも,引かれる数より答えが大きくなってしまっているからです。このような問題に出会った場合,逆算の関係から足し算に置き換えることで,足し算の虫食い算の応用として答えを導くことができます。例えばこの33-1□=17という問題だと,逆算では17+1□=33と置き換えられますよね。そしてこの問題において位ごとに作った式の不自然さから,繰り上がりが発生しているのだと考えることができます。したがって□の中身は7を足したら末尾が13になる一桁の数字である6と判断でき,答えは6だと分かりますね。このように繰り下がりが起きる問題では,足し算の式に考え直すことが有効です。
もちろん引き算特有の解き方も存在しないことはないですが,覚える攻略法は少ないほど効率がいいので,足し算に変形するというテクニックおよびその上で末尾に注目するという手法を意識しておくといいでしょう。
かけ算の虫食い算
それでは3つ目としてかけ算の虫食い算の解き方を説明していきます。例によって,この章でも例題を使いながら攻略の糸口を探っていきます。今回は3□×7=217という式を使っていきますので,一体どんな数字が当てはまるのか,一度自分の力でチャレンジしてみてください。
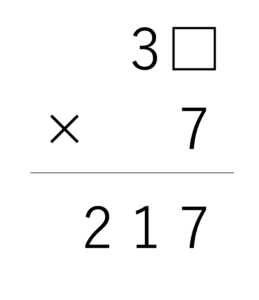
上のようなかけ算でも,基本的には位ごとの式を立てていくことで計算を進められます。
□×7=7
3×7=21
しかしかけ算の式ではほとんどの問題で繰り上がりが発生してしまうので,位ごとに考えていったところで□の中身が求めやすくなるかどうかは怪しいところです。そこで,位について着目するというポイントは変わらないのですが,かけ算の末尾に注目して□の中身を予測していくというテクニックをお勧めします。というのも,四則演算においていくら繰り上がり・繰り下がりが発生しようと,末尾つまりは一の位に限ってはかける数の一の位とかけられる数の一の位の積のみによって定まるからです。今回だと217という数字の末尾である7は,□×7の計算結果しか関わりのないところです。そのため□の中身を埋めていくのに最も適した着眼点だと言えるのです。今回の式において,7をかけると一の位が7になる一桁の数は1しかありません。そのため答えは1になります。
A.1
このようにして末尾に注目することで,かけ算の虫食い算は解きやすくなります。もちろん十の位も百の位も見落としてはいけませんが,一つの攻略法として意識していただくといいでしょう。
なお,今回は7をかけたら7になる数字が1しかありませんでしたが,この値が場合によってはいくつか考えられることがあります。例えば5をかけたら末尾が0になる数字などは山ほど選択肢がありますよね。2だと10に,4だと20に,6だと30に,8だと40になりますので,この場合4通りの選択肢があるわけです。このような場合は先頭の数の大きさをみながら適切なものを絞っていくといいでしょう。今回は基本編ということで深く解説しませんが,ともあれ位という軸を意識しながら解き進めてみてください。
割り算の虫食い算
最後に割り算の虫食い算の解き方を,同じように例題を用いながら説明していきます。今回は222÷□=7□という計算をもとに,割り算の虫食い算の解き方を学んでいきましょう。
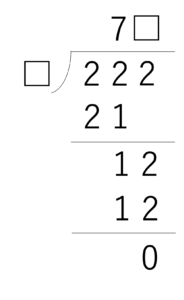
さて割り算の虫食い算のコツですが,筆算の構造が異なる以上なかなか位ごとの式を作るということは難しそうですね。しかし重要なのは変わらずそれぞれの位に着目してくことになります。ただしここで割り算に特有の性質として挙げられるのが,一番大きい位から考えていくということです。このポイントには割り算の筆算の手順が関わっています。足し算・引き算・かけ算の筆算は一の位から進めていきますが,割り算は大きいくらいから計算を始めていきますよね。そのため,問題によって手順に差があるとは言え,基本は大きいくらいに目を当てて考えていくとスムーズに計算できるでしょう。
今回だとまずは十の位の計算として,□に7がかけられていて,その結果として21という数字が導かれています。このことから逆算を利用すると,割る数の□には7をかけたら21になる一桁の数字である3が当てはまりますね。そしてこの3という計算結果に基づくと,商の□の中身も求めることができますね。3と□をかけた計算結果としてここでは12が登場していますので,□の中身は3をかけたら12になる一桁の数,すなわち4だと分かります。
A.3,4
このように計算を左から,つまりは大きい位から考えていくことで割り算の虫食い算はスムーズに解くことができます。もちろん□の数や位置によっては一の位などから考えていった方がやりやすい場合もありますが,基本的なテクニックとして大きい位からという意識で問題に向き合っていくといいでしょう。
練習用プリント(無料)
練習用プリント(無料)は、
『個別指導塾テスティー』の公式LINE の友だち追加された方のみの配布となっております。
以下から公式LINEの友だち追加をして、記事の続きをお楽しみください!!
≪入手方法≫
※画像はあくまでイメージです。本来送られるものとは違いますのでご了承いただけますよう、よろしくお願い致します。
①以下のリンクから公式LINEを友だち追加
②送信される画像をタップ!
パスワードで保護されている記事へと移動します。

③パスワードを入力(パスワードはLINEの友だち追加時に送信いたします。)
※パスワードを入力しても見ることができない場合、もう一度入力していただくか、キャッシュ機能の設定を変更するなどしていただきますよう、お願いいたします。

④スクロールしてPDFをダウンロード!

<スマートフォンからお読みの方はこちら>

<パソコンからお読みの方はこちら>
.png)
まとめ
今回は虫食い算のやり方やコツを紹介してきました。
その中でも「逆算」というワードが特に多く使われていたと思います。逆算は虫食い算を解くときに非常に重要になってきますので、是非自分のものにして、虫食い算を攻略していきましょう!