Contents
植木算とは? 問題のパターンとわかりやすい解き方
中学受験算数で頻出の特殊算の一つに「植木算」というものがあります。その名の通り、等間隔に植えられた木の本数を数える問題を解くときに使われます。応用問題も多数存在し、畑に植えた苗を数える問題や、のりしろのある紙をつないでいく問題などがよく見られます。
植木算は、受験算数では4 年生のカリキュラムとして教えられることが多いですが、実際の受験でもよく問われる分野の一つです。一度公式を習ってその場では理解したつもりでも、時間がたってから問題を解いてみると「植木算ってなんだっけ?」と思い、混乱してしまうことが多いです。あげくには、適当に1 を足したり引いたりして投げやりに解答を書いてしまうことに……。
しかし、植木算には重要なパターンがあることを理解し、落ち着いて問題に取り組めば、特殊算の中では比較的簡単に答えを導き出すことができます。受験本番になって後悔しないように、公式の暗記ではなく、考え方をきちんと理解しましょう。
今回はそんな植木算について、その考え方、問題を解くときのポイントと、受験生が押さえておくべき3つのパターンや応用問題をご紹介します。
植木算の考え方
植木算の問題には例えば次のようなものがあります。
「50 m の道路の片側に木を10 m 間隔で植えます。道路の両端にも木を植えるとすると、木は何本必要でしょうか。」
ここで、答えは50 ÷10 = 5 (本)と安直に考えたくなりますが、冷静になって考えてみましょう。まずは図を書いて考えてみることです。
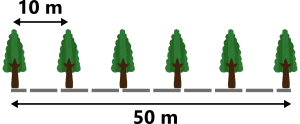
そうすると、先程の計算50 ÷10 = 5 で導き出された5 という数は、「木と木の間の数」だったことがわかります。道路の両端にも木を植えるため、植えた木の数は木と木の間の数から1 を足して、5 本だと分かります。
このように植木算の問題を解くときは、設問で与えられている「木の数」と「木と木の間の数」の関係を理解することが必要になります。
植木算の問題を解くときのポイント
植木算の問題を解くときは、先程の問題のように、図を書いて「木の数」と「木と木の間の数」の関係を理解することが重要です。植木算は、感覚的に解けそうで解けないからこそ受験参考書の単元の一つになっています。
状況がよく分からないまま直感的に答えを導き出すのではなく、問題文で与えられた状況を整理してから解くようにしましょう。
植木算の3 つのパターン
植木算の問題を解くポイントを押さえたところで、実際によく問われる植木算の問題にはどのようなパターンがあるかをご紹介します。
パターン1 直線状で、両端に木を植える場合
例「50 m の道路の片側に木を10 m 間隔で植えます。道路の両端にも木を植えるとすると、木は何本必要でしょうか。」
これは先ほど出てきた問題です。木と木の間の数は
50 ÷10 = 5
であり、図からわかるように、必要な木の本数は木と木の間の数より1 だけ大きく、6 本となります。
パターン2 直線状で、両端に木を植えない場合
例「50 m の道路の片側に木を10 m 間隔で植えます。道路の両端には木を植えないとすると、木は何本必要でしょうか。」
今度は両端に木を植えないパターンです。この場合にも、図を書いて「木の数」と「木と木の間の数」の関係を理解しましょう。

すると、この場合は必要な木の本数は木と木の間の数より1 だけ小さく、
50 ÷10 - 1 = 4 (本)
となります。
パターン3 池の周囲などに木を植える場合
例「周囲が50 m の池の周りに、木を10 m 間隔で植えます。木は何本必要でしょうか。」
今度は直線状ではなく、木を円周上に植えます。図を書いてみましょう。
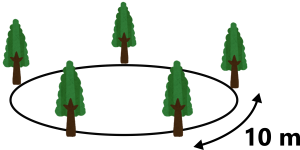
図からわかるように、この場合は「木の数」と「木と木の間の数」が等しくなります。したがって、必要な木の数は5本です。
のりしろのある紙をつないでいく問題
さて、植木算の考え方と、重要な3 つのパターンについて説明が終わりました。これらを使って、植木算を応用した問題を解いてみましょう。
応用問題「長さ6 cm の細長い紙を、のりしろを1 cm としてまっすぐ5 本つなげました。全体の長さは何cm になるでしょう。」
全体の長さを求めるために、まずはのりしろの数を数えてみましょう。図を書くと以下のようになります。

これは、両端に木を植えない場合、すなわち先ほどのパターン2 に当てはまることが分かります。このとき、のりしろの数(=木と木の間の数)は紙の枚数(=木の本数)よりも1つだけ少ない4つとなります。
全体の長さは、紙の全長からのりしろの全長を引けばよいため
6 ×5 -1 ×4 = 26 (cm)
と求めることができます。
まとめ
今回は植木算について説明しました。内容をおさらいすると、まず図を書いて「木の数」と「木と木の間の数」の関係を理解します。また、その関係が今回紹介した3つのパターンのうちのどれに当てはまるかを考えることで、正解を導き出すことができます。
特殊算の問題は様々なパターンの問題を繰り返し練習することで、得意分野にすることができる確率が高いです。この機会に植木算をマスターしてしまいましょう!
<関連記事>















