この記事では「いもづる算」の解き方を解説していきます。問題を一緒に考えながら、基本の解き方と工夫の仕方を学んでいきましょう。
Contents
いもづる算とは
いもづる算はつるかめ算と似ていますが、条件がつるかめ算よりも少なく、答えが複数でることがあります。
答えが複数ある時は、何通り答えがあるかが問われることが多いです。条件によっては答えが1つに定まる時もあります。
これでは想像しにくいかもしれないので、例題を見てみましょう。
-
1個120円のりんごと1個80円のみかんを何個かずつ買ったところ、代金は720円でした。りんごとみかんの買い方は何通りあるでしょうか。ただし、どちらも1個ずつは買うものとする。
-
1個167円のりんごと1個70円のみかんをいくつかずつ買ったところ、代金は1492円でした。りんごとみかんをそれぞれ何個ずつ買ったでしょう。
-
1個120円のりんごと1個83円のみかんと1個135円のレモンをいくつかずつ買ったところ、その合計金額は2786円であった。みかんを何個買ったでしょう。ただし、りんごをレモンの5倍だけ買ったとする。
例えば①の問題で、りんごとみかんを合計で何個買ったか分かっていればつるかめ算となり、りんごとみかんの買い方は1通りに定まります。
しかし、ここではりんごとみかんの合計個数が分かっていないため、何通りかの買い方が考えられます。
これが「いもづる算」です。ここからは実際に問題を解いていきましょう。
いもづる算の解き方
まずは、問題①を解きながら基本を学んでいきます。
(問題①)1個120円のりんごと1個80円のみかんを何個かずつ買ったところ、代金は720円でした。りんごとみかんの買い方は何通りあるでしょうか。ただし、どちらも1個ずつは買うものとする。
「りんごが\(120\)円、みかんが\(80\)円、合計\(720\)円」とわかったら、まず何をすればいいでしょうか?
この情報がわかったら、まずは何個まで買えるのかを調べてみましょう。例えば、みかんはとりあえず置いておいて、りんごを\(100\)個買うことは出来るでしょうか?\(10\)個はどうですか?\(5\)個ならどうでしょう?
\(100\)個買うとしたら、\(120\)(円)\(\times100\)(個)\(=12,000\)(円)になってしまうので買えませんね。\(10\)個も\(1,200\)で無理ですが、\(5\)個なら\(600\)円で買えそうです。このように何個まで買えるのかを最初に考えると、数が絞れて解きやすくなります。実際は合計金額をりんご\(1\)つの値段で割って求めます。\(720÷120=6\)より、りんごは最大でも\(6\)個しか買えません。
この問題では「りんごもみかんも\(1\)個ずつは買う」という条件があるので、\(0\)個のときは除いて\(1~6\)個買うとわかります。(りんごを\(6\)個買うときも、みかんが\(0\)個になるのでダメなのですが、今回は入れておきます。ここで除いても大丈夫です。)
ここまでわかったら、ここからは「しらみつぶしに解く」と「工夫して解く」の2通りの解き方で考えてみましょう。
解き方① しらみつぶしに解く
しらみつぶしに解くといっても、やみくもにいろいろ試して\(720\)円になるのを探すようなやり方ではいけません。それだと数え忘れていても気づきにくいからです。しっかりと全ての場合を調べましょう。
ここでは\(720\)円になる可能性のあるりんごの個数が\(1~6\)個だと分かったので、それぞれの時のみかんの個数を調べたら全ての場合を調べたことになります。りんごが\(7\)個以上のときは\(720\)円にはならないので調べても意味がありません。

注:みかんの個数は整数にならないといけないので整数にならなかったものには×と書いています。例えば、りんごの個数が\(1\)個の時、みかんの個数は\(600÷80=7.5\)となるので×となります。
先ほどもちょっとお話ししましたが、みかんも最低\(1\)個は買うと問題文にあるため、みかんが\(0\)個の場合もここで除きます。
以上より、(りんごの個数、みかんの個数)\(=\)(\(2,6\))、(\(4,3\))の\(2\)通りだと分かります。
この解き方は確実ですが、ものの個数が多くなると手間がかかり解くのに時間がかかってしまいます。
余談ですが、ここでみかんではなくりんごの個数の範囲をしぼったのには意味があります。りんご同様にみかんの個数をしぼると、\(720÷80=9\)となりみかんの個数は\(1~9\)個だと分かります。これだとりんごの個数を\(9\)通り調べる必要があり、りんごの個数をしぼった時の\(6\)通りよりも手間がかかります。
数をしぼるときは、割る方の数(今回は\(1\)個の値段)が大きい方で割ると解きやすくなるので、気にしてみるといいかもしれません。
解き方② 工夫して解く(りんごをみかんにおきかえる)
さて、次は工夫して解いてみます。今回のような簡単な問題だとしらみつぶしの方が楽かもしれませんが、難しくなると工夫が必要になるので 練習しましょう。
「りんごが\(120\)円、みかんが\(80\)円、合計\(720\)円」から、今回はそれぞれの数に注目してみます。
りんごの値段である\(120\)円とみかんの値段である\(80\)円の最小公倍数は\(240\)なので、りんご\(2\)個とみかん\(3\)個の値段は同じです。(\(120×2=80×3=240\))
「いきなり最小公倍数なんて思いつかないよ!」という方も多いかと思いますが、ここで知って、次違う問題で思い出せれば良いと思います。
(私は工夫して解くのが苦手なので、こんな工夫の仕方があるよとご紹介して、どんどん吸収していただければと思っています。)
話を戻すと、「りんご\(2\)個=みかん\(3\)個」なので、置き換えることができそうです。りんごを\(6\)個買うと\(120×6=720\)(円)なので、ここから置き換えてみましょう。
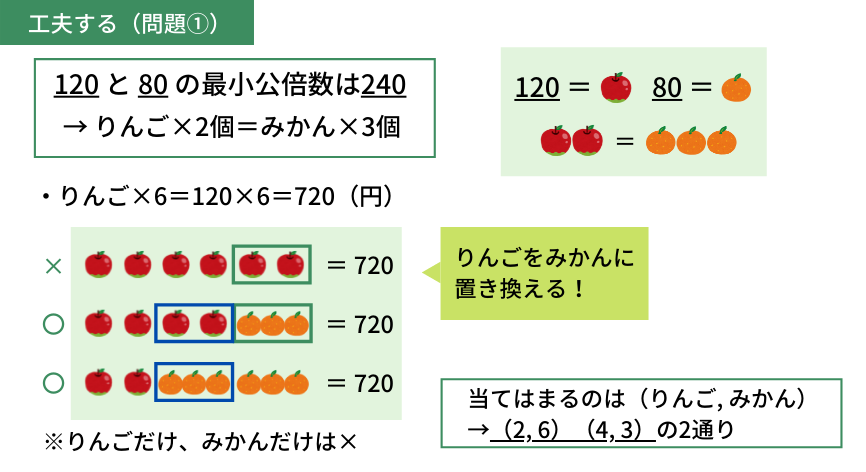
りんご\(2\)個をみかん\(3\)個に置き換えても値段は変わらないので、(りんご, みかん)\(=\)(\(6, 0\))、(\(4, 3\))、(\(2, 6\))、(\(0, 6\))のときは全て\(720\)円になりますね。(上の図参照)
ただし、「りんごもみかんも\(1\)個ずつは買う」という条件があるので、(\(6, 0\))と(\(0, 6\))のときは除きます。
よって、(りんご, みかん)\(=\)(\(4, 3\))、(\(2, 6\))の\(2\)通りの買い方があることが分かります。
問題に慣れよう
次に、もう少し難しい問題を解いてみましょう。
(問題②)1個167円のりんごと1個70円のみかんをいくつかずつ買ったところ、代金は1492円でした。りんごとみかんをそれぞれ何個ずつ買ったでしょう。
この問題は、しらみつぶしで解くこともできますが、あることに気がつくと早く解くことができます。まずはしらみつぶしで解いてみましょう。
解き方① しらみつぶしに解く
先ほどと同じように、まずはりんごの個数をしぼりましょう。1492÷167=8.93・・・なので、りんごを\(9\)個以上買ってしまうと\(1492\)円を超えてしまいます。
つまり、りんごの個数は\(0~8\)個です(「りんごとみかんをそれぞれ\(1\)個以上買う」という条件はないので\(0\)個の場合も考えましょう)。
では、それぞれの場合についてみかんの個数を求めてみましょう。

りんごの個数を変えて残高を計算していくと、\(490\)円(りんごが\(6\)個のとき)以外は\(1\)の位が「\(0\)」ではありませんね。
みかんは\(70\)円なので、\(1\)の位が「\(0\)」でないと割り切れません。そのため、みかんの個数が整数になるのは、りんごが\(6\)個、みかんが\(7\)個のときだけとわかります。
解き方② 工夫して解く
「りんごが\(167\)円、みかんが\(70\)円、合計\(1492\)円」と見て、何か工夫できそうなところはありますか?
先ほどの問題は最小公倍数で考えましたが、今回の数字は\(1\)の位が「\(7\)」や「\(2\)」できりが悪いですね。ここが使えそうです。
合計の\(1\)の位は「\(2\)」ですが、みかんの\(1\)の位は「\(0\)」なので何個買っても\(1\)の位は変わらなそうです。そのため、りんごの合計金額の\(1\)の位が「\(2\)」となる個数である必要があります。
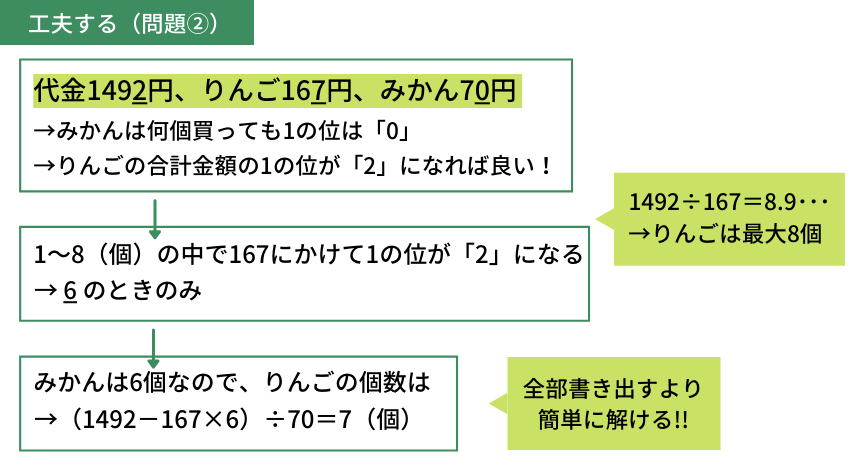
ここで、りんごの個数は\(1492÷167=8.93\)・・・で\(0~8\)個です(「しらみつぶし」参照)。ただし、全部みかんのときは\(1\)の位が「\(0\)」なので、りんごが\(0\)個のときは除きます。
\(167\)に\(1~8\)(個)をかけて\(1\)の位が「\(2\)」になるのは、りんごの個数が\(6\)個のとき。以上より、りんごは\(6\)個だとわかります。みかんの個数は\((1492-167×6)÷70=7\)(個)です。よって、求める個数はりんご\(6\)個、みかん\(7\)個です。
いもづる算の解き方のまとめ
ここまででご紹介した解き方をまとめると、このようになります。
- 工夫できるか考える
- 個数の範囲をしぼる
- しらみつぶしで考える
「問題文の数字を書き出したい」「個数の範囲は最初に計算したい」などがあれば、解きやすい順番に変えてみてください。
いもづる算の応用
最後に、ご紹介した解き方を使って応用問題を解いてみましょう。
(応用問題)1個120円のりんごと1個83円のみかんと1個135円のレモンをいくつかずつ買ったところ、その合計金額は2786円であった。みかんを何個買ったでしょう。ただし、りんごをレモンの5倍だけ買ったとする。
①工夫できるか考える
今までのように単純にレモンの個数をしぼると、\(2786÷135=20\)・・・となり、レモンの個数は\(0~20\)個となってしまいます。さらに、それぞれの場合においてりんごとみかんの個数も考える必要があり、非常に手間がかかってしまいます。
では、他に使えそうな条件はあるでしょうか?「りんごをレモンの\(5\)倍だけ買う」という条件に注目してみましょう。
これを言い換えると、「りんご\(5\)個とレモン\(1\)個を、セットで買う」ということになります。
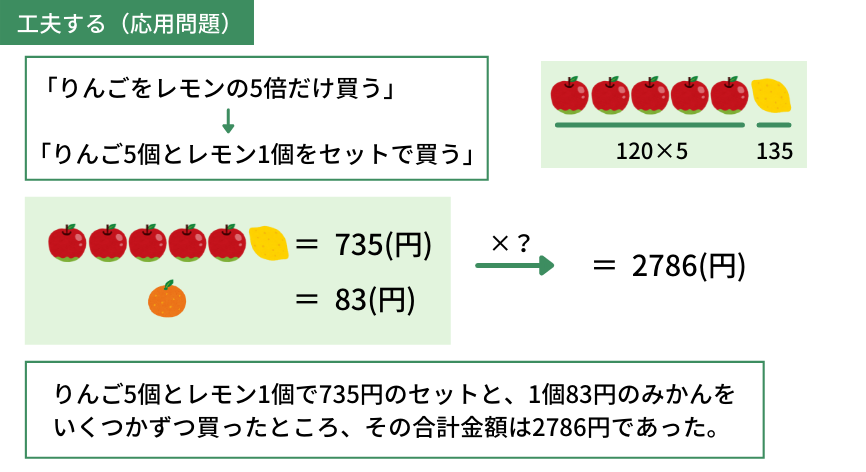
りんご\(5\)個とレモン\(1\)個の合計金額は\(735\)円です。(\(120\times5+135=735\))
今わかったことで問題文を書きかえてみると、下のようになります。
(応用問題:書き換え)りんご5個とレモン1個で735円のセットと、1個83円のみかんをいくつかずつ買ったところ、その合計金額は2786円であった。みかんを何個買ったでしょう。
これで最初に解いた問題①とほとんど同じ問題になりました。
②個数の範囲をしぼる
りんご\(5\)個とレモン\(1\)個のセットは、\(2786÷735=3.79\)・・・より\(0~3\)セットです。あとはそれぞれの場合でみかんの個数を調べればいいですね。
③しらみつぶしで考える
では、それぞれの場合のみかんの個数を調べましょう。

上の表からみかんの個数は\(7\)個だと分かります。
練習用プリント(無料)
練習用プリント(無料)は、
『個別指導塾テスティー』の公式LINE の友だち追加された方のみの配布となっております。
以下から公式LINEの友だち追加をして、記事の続きをお楽しみください!!
≪入手方法≫
※画像はあくまでイメージです。本来送られるものとは違いますのでご了承いただけますよう、よろしくお願い致します。
①以下のリンクから公式LINEを友だち追加
②送信される画像をタップ!
パスワードで保護されている記事へと移動します。

③パスワードを入力(パスワードはLINEの友だち追加時に送信いたします。)
※パスワードを入力しても見ることができない場合、もう一度入力していただくか、キャッシュ機能の設定を変更するなどしていただきますよう、お願いいたします。

④スクロールしてPDFをダウンロード!

<スマートフォンからお読みの方はこちら>

<パソコンからお読みの方はこちら>

まとめ
いかがでしたか。いもづる算は難しい問題だと工夫の仕方が大切になってきます。
苦手だと思う方も、色んな問題を解いて慣れれば解けるようになります。この記事が少しでも参考になれば嬉しいです。

















