今回の記事では,前回の基礎編に引き続き時計算についてご紹介していきます。時計算はそのテーマから「所詮時計でしょう」と甘くみられがちですが,その本質は旅人算や通過算といった速さに関する問題と同じなので,受験生の多くが時計算に苦戦してしまいがちです。そのため早いうちからの対策が欠かせません。今回は受験本番を想定した攻略法をご紹介していきますので,ぜひ一読いただけますと幸いです。
Contents
基礎編の振り返り!時計算とは?
まずは基礎編の振り返りとして時計算とはどのような文章題かを確認していきましょう。この章の内容を思い出せなかったり耳にしたことがなかったりした場合には前回の記事に改めて目を通していただけますと幸いです。
さて,時計算とは端的に言ってしまえば時計の短針と長針の作り出す角度に関する問題のことを意味しました。時計の短針は12時間で1周360°動く,つまり1時間で30°・1分間で0.5°進んでいきますが,他方長針は1時間で1周しますので1分間で6°動くことが分かります。そしてこの2つの針が同じ方向に進んでいますので,旅人算の要領で考えると,長針と短針の作る角度は1分間に5.5°変化すると言えます。この2つの針の動き方は時計算を解く上で必須の知識ですので,ぜひ覚えておきましょう。今回の記事でご紹介する問題を演習する際には,この章の内容を見ながら解いてみるのもいいかもしれません。
またこれらの針に関する事項だけではなく,基礎編の記事では時計算という文章題を解く上で抑えておきたいポイントをいくつかご紹介しましたね。その一つが時刻を図に表すというものです。時計の動き方を頭の中だけでイメージすることは難しいと思われるので,慣れるまでは丁寧に時計の図を書くことで問題に取り掛かりやすくしましょう。もう一つのポイントが,答えが分数になることもあるということです。普段,時刻というものは整数で表されるのですが,この時計算においては話が変わってきます。\(3時16\frac{4}{11}分\)などといったように,計算の結果〇〇分の部分が分数になることも少なくありません。初めのうちは戸惑ってしまうでしょうが,そういうものだと割り切って答えていきましょう。
問題① 時刻から角度を求める問題!
ここからは本題の演習に移ります。図を正確に書くことを意識すると解きやすいかと思われますので,その点に注意しながら挑戦していただけますと幸いです。
次の□にあてはまる数を求めなさい。
時計が2時50分を示しています。長針と短針がつくる小さい方の角の大きさは□°です。
(成城学園中学校(2016),一部改題)
解説①
それでは1問目の答え合わせをしていきましょう。基礎編と上の振り返りでご紹介した攻略手順に沿って解き進めていきましょう。今回の問題はある時刻の時計が作り出す角度を問う問題でした。時計算にはこのタイプの問題と,ある角度を作り出す時計の時刻を問う問題とが存在するのですが,このうち前者はキリのいい答えになりやすいので幾分か解きやすいのではないでしょうか。今回の問題では2時50分という時刻が与えられていたので,まずはその時刻を図に表してみましょう。今回起こりがちなミスが,短針が2時ぴったりを指すと考えてしまうことです。時計の短針も,2時0分から50分までの間にいくらか進んでいるということを忘れずに図に書き起こしましょう。
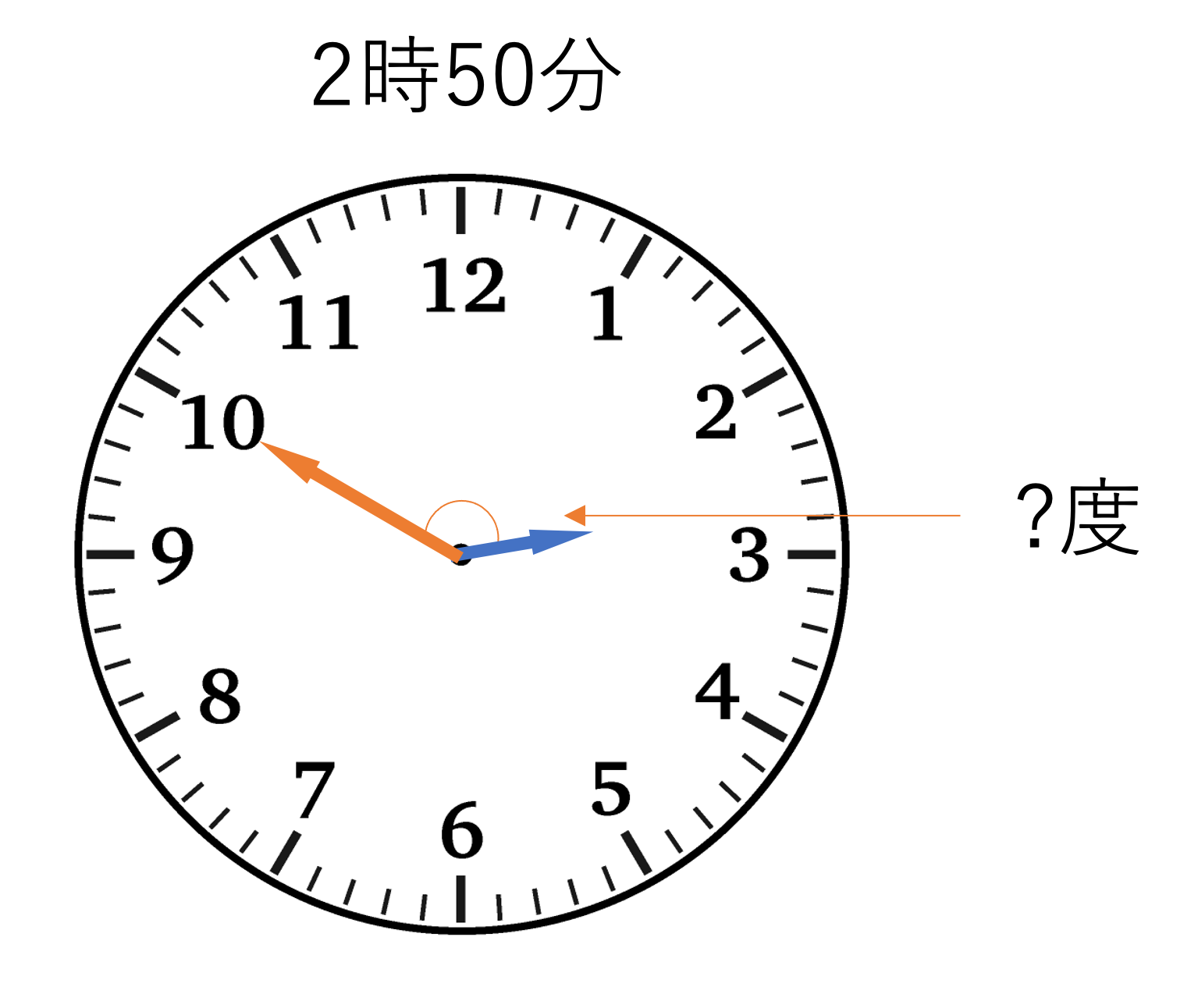
この図から,今回求めればいいのは時計の10から2までで作られる角度だということがわかります。ここで時計の2つの針における1時間の差が作り出す角度は,360°を12等分しているので30°になることを思い出しましょう。つまり,2つの針が1時間分離れていれば30°,2つ離れていれば60°といった具合で角度が増えていくわけです。ただ,今回の時刻では短針が2と3の間にいるため,30°というキリのいい大きさで考えていくことには限界があります。ここで大切になるのが,角度を1時間の差のかたまりと針が動いた角度に分けることです。このステップを踏むことで,問題の答えを正確に導くことができます。今回は2時50分の時に作られる角度を,10と2の間というキリのいい角度と短針が2から3までで動いた角度とに分けて計算していきましょう。
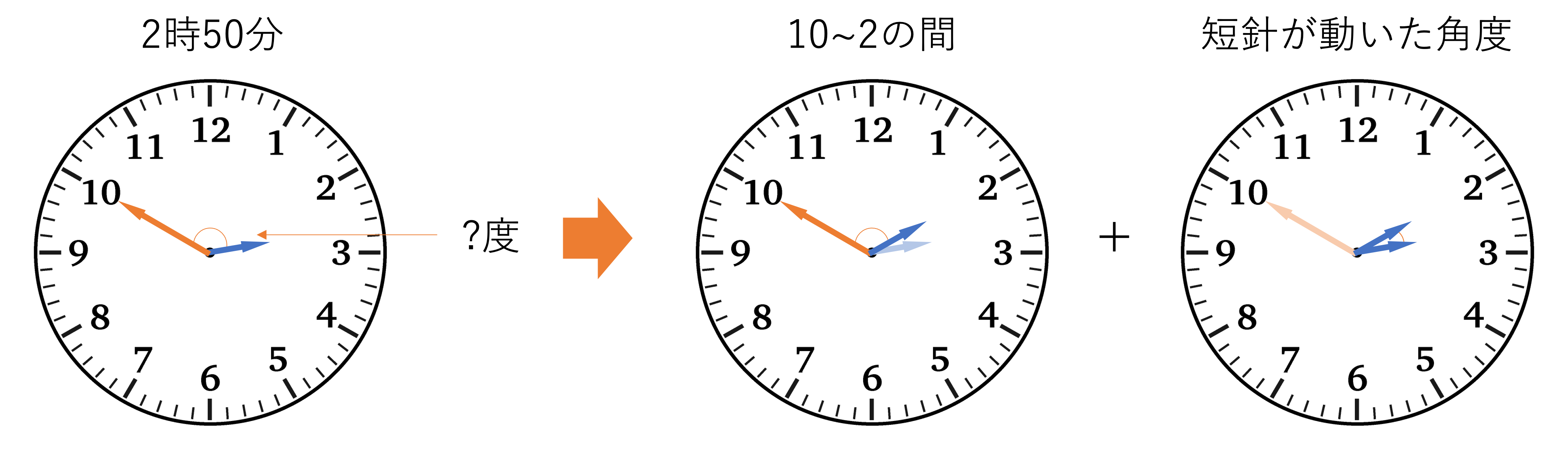
このうち前者から考えていきます。10から2の間で作られるというのは30°のかたまりが4つ集まったものと見なせますね。したがって30°×4=120°となります。
続いて短針が動いた分の角度について考えていきましょう。先ほど申し上げたように短針は1分間に0.5°動きます。今回の問題において,短針の位置を2時ジャストから50分動いたものと考えると,2の位置から0.5°×50=25°離れていることがわかります。それゆえ短針が動いた角度は25°となるわけです。
そしてこれらの角度を足し算すると,145°になります。したがって2時50分のときに長針と短針が作り出す角度は145°となるわけです。このように,ある角度をキリのいい部分と針が動いた部分に分けることは計算を簡単にしてくれます。今回は長身が10の位置ぴったりにあったので単身の動きのみを考えましたが,もちろん長身の位置が時計のどの数字の位置とも被らない場合は長身の動きについて考えていく必要があるので,そのような問題に出会ったときは気をつけていきましょう。
A.145°
問題② 角度から時刻を求める問題!
続いては先ほどご紹介した時計算と反対のパターンである,角度から時刻を求める問題です。中学入試で登場する時計算のほとんどはこの形の問題になるので,早いうちから慣れておくという意識で解いてみてください。
次の□に当てはまる数を入れなさい。
7時と8時の間で,時計の短針と長針が重なるのは7時○分です。
(学習院中等科(2020),一部改題)
解説②
それでは解説に移ります。この問題でも,まずは与えられている時刻を図に表すことから始めていきましょう。今回は7時から8時までと言われているので,7時の時計と8時の時計,加えてその間で長針と短針が重なるときの時計の3つを並べてみると分かりやすくなるでしょう。
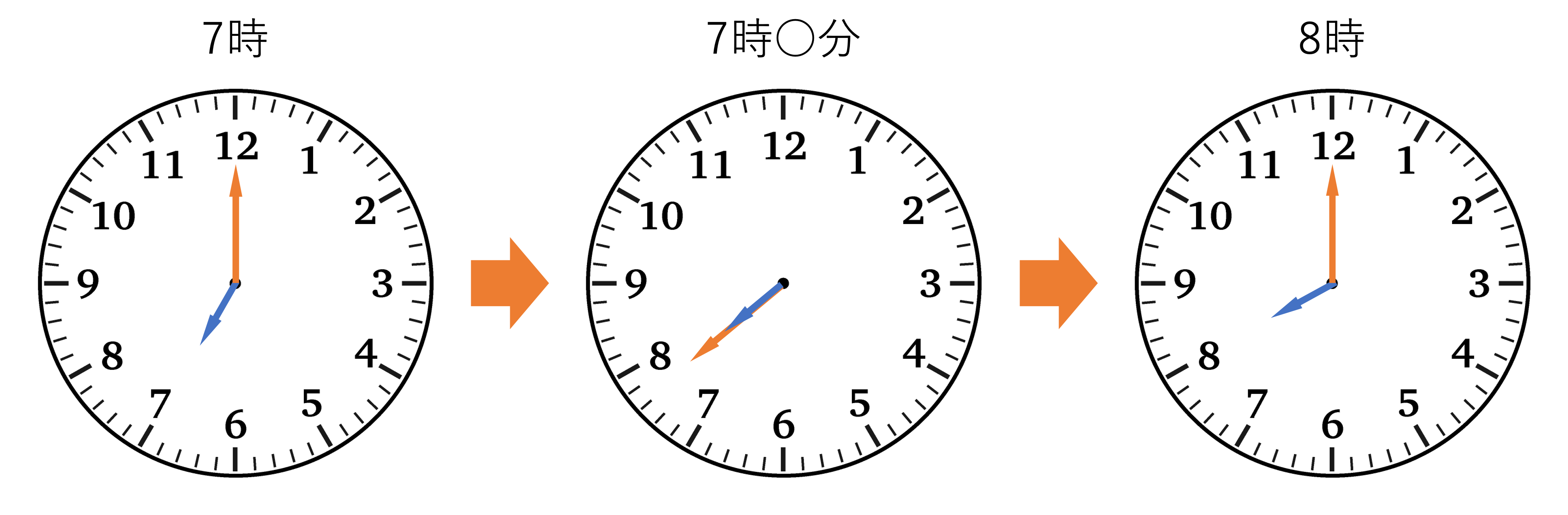
このような図を書き上げることができたら,今度は長針と短針の動き方や重なるときの条件について考えていきましょう。まず長針については,当たり前ですが時計を一周します。他方短針については,7と8の間を動きます。そのため2つの時計の針がぴったり重なるのは7時台のどこかであり,しかもこのとき2つの針が重なるためには長針も7と8の間にいなければいけないことから,針が重なる時刻は7時35分から7時40分までのどこかということまで推測できます。この予想をもとに答えを考えていくといいでしょう。
ここからは肝心の計算方法ですが,ここで2つの針が作り出す角度の大きさに注目してみましょう。いま7時から8時になるまでの角度の変化の仕方を考えると,7時のときに作り出される角度は次第に小さくなり,7時○分で0°に到達し,そこからは角度が開いていくという流れが分かります。そのためこのような問題では,元々2つの針が作り出していた角度を基準とし,1分あたりに変化する長針と単身の角度と照らし合わせながら,その角度が0になるまでにかかった時間を算出していけばいいですね。
今回の問題は7時ちょうどをスタートとしています。そのため元々2つの針が作っていた角度は30°×7=210°になります。なお,ここでは角度が小さくなっていくという流れに基づいて計算を進めているため,2つの針が作る大きな方の角を元々の角度としています。そして上で見たように,1分間で長針と短針のなす角は5.5°ずつ変化していきます。つまり7時1分には角度が204.5°に,7時2分には角度が199°に,……と小さくなっていくわけです。このようにして7時から何分後に針がぴったり重なるかを考えると,次のような式が立てられ,これを解くと答えが求められます。このとき答えが帯分数になりますが,時計算では頻繁にあることですので,自信を持って答えましょう。
\(210°÷5.5°=\frac{210}{5.5}=\frac{420}{11}=38+\frac{2}{11}\)
したがって2つの針がぴったり重なるのは7時の\(38\frac{2}{11}\)分後だと分かります。ちなみにこの7時\(38\frac{2}{11}\)分というのは,7時38分と7時39分の間を指しますので,上で確認した7時35分から7時40分の間という条件を満たすことになります。このように答えにアタリをつけておくと簡単に確かめ算を行えますので,余裕がある人は答えを予測する癖をつけておきましょう。
A.\(38\frac{2}{11}\)分
問題③ 秒まで考える時計算!
最後にご紹介するのは秒数まで考えなければならない時計算です。これまでの問題より考える要素が増えるため悩むこともあるかと思いますが,基本的な要素は上で見た2つの問題と同じです。基礎に忠実に解いていきましょう。
3時から4時の間で,時計の短針と長針がつくる角が90°になるのは3時何分何秒ですか。割り切れない時は秒の単位を帯分数で答えなさい。ただし,3時は除きます。
(森友学園中学校(2018),一部改題)
解説③
それでは最後の問題の解説に移りましょう。今回の問題も時刻を図に表すことから始めていきましょう。この問題では3時から4時までの時計の動きについて考えなければいけないので,3時と4時,それから3時台で長針と短針が90°の角を作るときの時刻の3つを書き出しましょう。
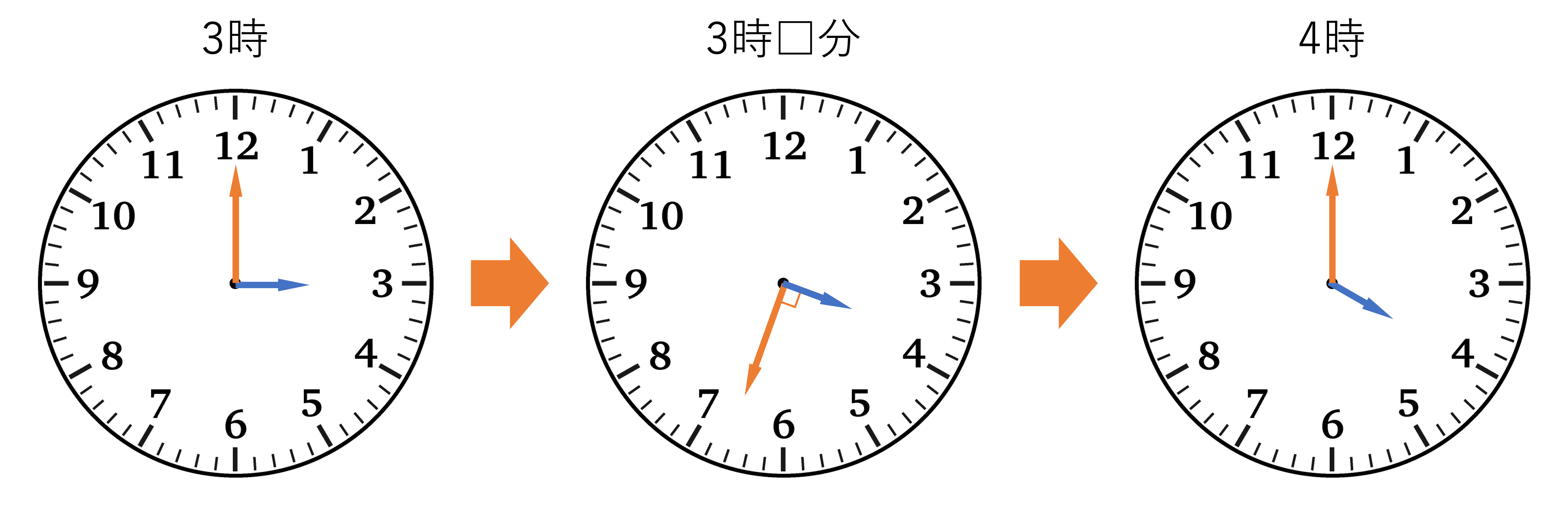
このように図を書くと,短針が3時から4時までの間を動くということから,長針のなんとなくの位置も推測できますね。時計の3の位置から90°離れているのは6の地点,時計の4の位置から90°離れているのは7の地点なので,長針は6と7の間の位置を指しているだろうと予測できるわけです。つまり答えが3時30分から3時35分の間になるだろう,とアタリがつけられますね。この結果は確かめ算のときに使えるので,前述したように余裕がある人は予測することを習慣にしておくといいでしょう。
ここからは2つ目の問題と同様の手順で進めていきます。この問題についても,時計の短針と長針がなす角度の大きさの変化について見ていきましょう。3時ぴったりのときに作り出される角度は時間が経つにつれて小さくなり,3時のどこかで0°に到達し,そこからは角度が開いていくという流れが分かります。今回は元々の角度が90°であり,2回目に90°になるときの時刻を求める必要がありました。このことから作られる角度が90°に達するときの時刻は,一度針同士がぴったり重なって再度角度が大きくなってからになる,つまり角度は90°→0°→90°と動くと判断できます。それゆえ2つの針が作り出す角度は合計で180°変化するわけですね。そのため180°動くのにかかった時間が,今回の問題の答えになるわけです。
ここで時計の短針と長針が作り出す角度は1分間に5.5°変化するということから,どれくらいの時間で90°の角が出来上がるか,に関する式を立てて計算することができそうです。今回は下のような式を立てて計算するとその答えが求まります。
\(180°÷5.5°=\frac{180}{5.5}=\frac{360}{11}=32+\frac{8}{11}\)
ということで3時から\(32\frac{8}{11}\)たった時間,つまり3時\(32\frac{8}{11}\)分に2つの針のなす角が90°になるわけです。ただここで注意しなければいけないのが,今回の問題では秒数まで計算しなければならないということです。この問題の答えである\(32\frac{8}{11}\)という帯分数において,秒数を指すのは\(\frac{8}{11}\)の部分です。\(\frac{8}{11}\)分というのは秒数に直すと次のようになります。
\(\frac{8}{11}[分]= \frac{8}{11}×60[秒]= \frac{480}{11}[秒]=43\frac{7}{11}\)
したがって先ほど求めた答えを書き直して求められている正確な形に直すと,答えは32分43\(\frac{7}{11}\)秒後ということになります。時計算ではこのように秒数まで計算しなければいけないこともあるので,求められている単位には気をつけましょう。また,単位だけでなく回答の形にも注意する必要がありますね。時刻で答えるべきなのか,それともかかる時間を答えるべきなのか,しっかり判断して×をつけられないようにしましょう。
A.32分43\(\frac{7}{11}\)秒
終わりに
今回の記事ではこれまで,実際に入試で出題された問題を引用しながら時計算の解き方についてお教えしてきました。攻略法の中には時計算だからこそ必要となる知識もあれば,算数の文章題全般に当てはまるテクニックもあります。ぜひ今後の演習で活用してみてください。よろしければおすすめ記事や参考書などを使いながら,更なる学力向上を狙っていただけますと幸いです。

















