今回の記事は還元算・相当算についての記事となっています。初級編では,そもそも還元算・相当算とは何かという話から□のある計算の方法などについて,考え方のコツを交えながらご紹介していきました。今回はもっと応用的な内容に踏み込んでいきます。よろしければ一読してみてください。
還元算・相当算とは?基礎編のおさらい!
まず基礎編で解説してきたことを軽く確認していきましょう。そもそも還元算・相当算とはどのようなものを指したか,ちゃんと覚えられていますか?還元算・相当算というものは□が使われる式を作る必要のある文章題を意味しましたね。前回の記事ではその前段階として,□のある四則演算の解き方を確認していきました。
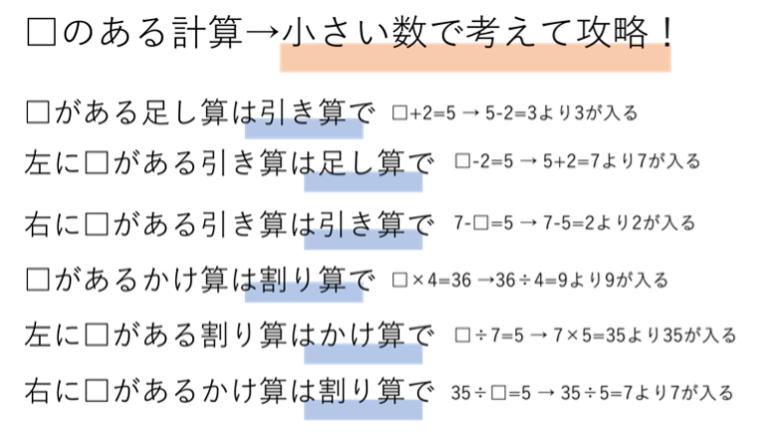
今回の中級編・次回の上級編では,この□の入っている式の解答の導き方が分かっている前提で解説を進めていきます。そのため,もし不安な人がいれば前回の記事を振り返ったり学校の教科書を見たりして確認しておくといいでしょう。ここで,前回お教えしたテクニックを再掲しておきます。小さい数をもとに考えるという考え方はぜひ今のうちに思い出しておいてください。
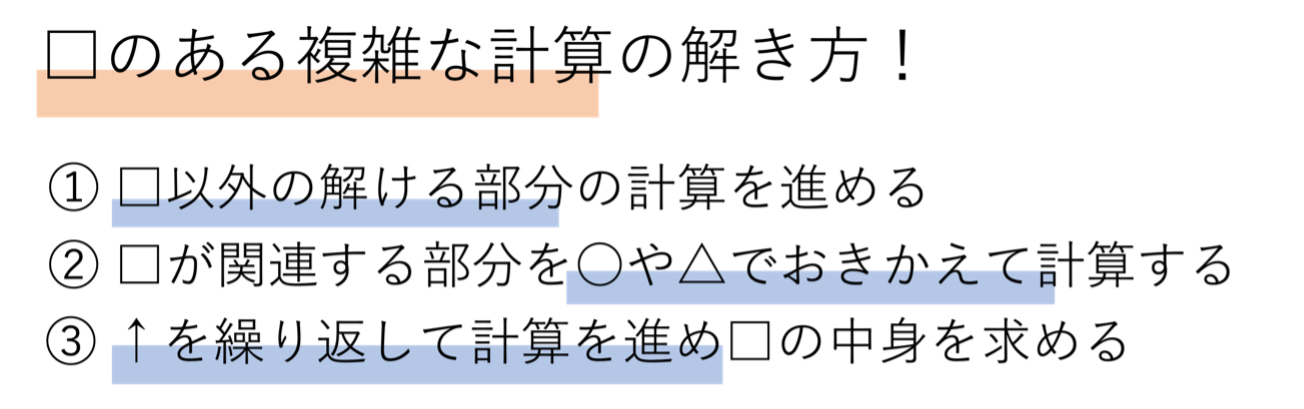
また□の含まれる複雑な計算に出会ったときの対処法もご紹介しましたね。それは□以外の解けるところから解いていく,そして□が含まれる部分を別の文字で置いて段階的に計算を進めるという方法でした。慣れてしまえばこのような回りくどい計算方法を取らなくてもいいのですが,ややこしい計算が簡単に解けるようになるまでは是非このやり方で問題に向き合ってみってください。
還元算・相当算の例題をご紹介!
それではここからは,今回の記事の本題であるところの還元算・相当算という文章題の攻略法についてお教えしていきます。ただ,まずは問題の解き方そのものを見るのではなく,例題をもとにどんな要素が登場してきているのか,還元算・相当算だと見分けるポイントはどこなのかを考えていきましょう。早速ですが,還元算・相当算の文章題をいくつか取り上げていきます。
ある本を1日で全体の15%読んだ。次の日に残りの40%を読むと50ページ残った。この本のページ数は何ページでしょう?
水筒の水を姉が最初に30%飲み,次に弟が100mL飲んだので,水の量は元の30%になった。この水筒には,何mLの水が入っていたでしょう?
ゆきお君とちひろさんの所持金の比は4:3で,ゆきお君がちひろさんに300円あげるとその比は5:7になるという。2人の所持金をそれぞれ求めなさい。
ちなみにこのような問題に,原価や定価・何割引きといった要素を加えたさらに難しい問題も中学受験では登場するのですが,今回の解説シリーズではそこまで触れません。気になる方は参考文献などで調べてみてください。
注目するポイントは〇〇
では上で見た3つの例題から分かることにはどんなものがあるでしょうか,一緒に考えていきましょう。ここで共通している点は,どれも数と割合という2つの指標が登場しているということです。第一問であれば15%・50ページ,第二問であれば30%・100mL,第三問であれば4:3・300円,といったような異なる表し方の数字が登場しています。実は還元算・相当算を見分けるポイントはこの2つの異なる指標が存在するかどうか,という点にあります。そして数字または割合の部分が別の表し方だとどのようになるか,別の言い方をするとどのくらいに相当するかを考えていくので相当算と呼ばれるわけです。
そして2つの基準や指標が登場するということは,2つの異なる指標を1つにまとめて考えていけば問題が解けるような構造になっているということであり,そのために有効な考え方が線分図というわけです。このことから,以下では還元算や相当算を解く上で覚えておきたい線分図の書き方をお教えしていきます。そんなの知ってるよ,という人は飛ばしてもらっても構いませんが,線分図は中学受験の一番の基礎となる部分なので,ぜひ復讐のつもりで読んでみてください。
線分図の書き方を覚えよう!
そもそも線分図とはどんなものを指すのでしょうか。線分図とは1本の線を基準として,その線におけるある部分が全体のどれくらいに当たるかがわかりやすいように図にしたものです。試しに先程ご紹介した問題の一問目を使いながら,線分図に関係を整理するとどうなるか考えていきましょう。
ある本を1日で全体の15%読んだ。次の日に残りの40%を読むと102ページ残った。この本のページ数は何ページでしょう。
線分図を書く上でまず大切なことが,全体を示すものは何かを把握することです。全体というと分かりづらいかもしれませんが,問題の基準というと伝わるでしょうか。今回の問題では本のページ数というのが全体に当てはまりますね。それは,本全体のページ数というものを基に,15%や102ページという単語が登場しているからです。
それではこの本全体のページ数を基に,線分図を書いてみましょう。まず線分図の基礎である線の長さは本のページ数を表しますので,そのことを線と一緒に記しておき,答えを考えやすいようにしておきましょう。そしてその下に,還元算・相当算に特有の2つの基準で計られた量を書きましょう。今回の問題では,割合とページ数という2つの基準で読んだ量や残りの量が表現されていました。このような要素を,下の図のようにまとめてあげましょう。なおこのとき,15%というのが全てのページ数の15%ではなく,1日目で読んだ40%を引いた残りの量の15%だということを正確に抑えておきましょう。なお,現段階でわからない初日に読んだページ数や2日目に読んだページ数は,□や△で表します。このように分からない量を一旦無視して図を書く,ということも大切です。
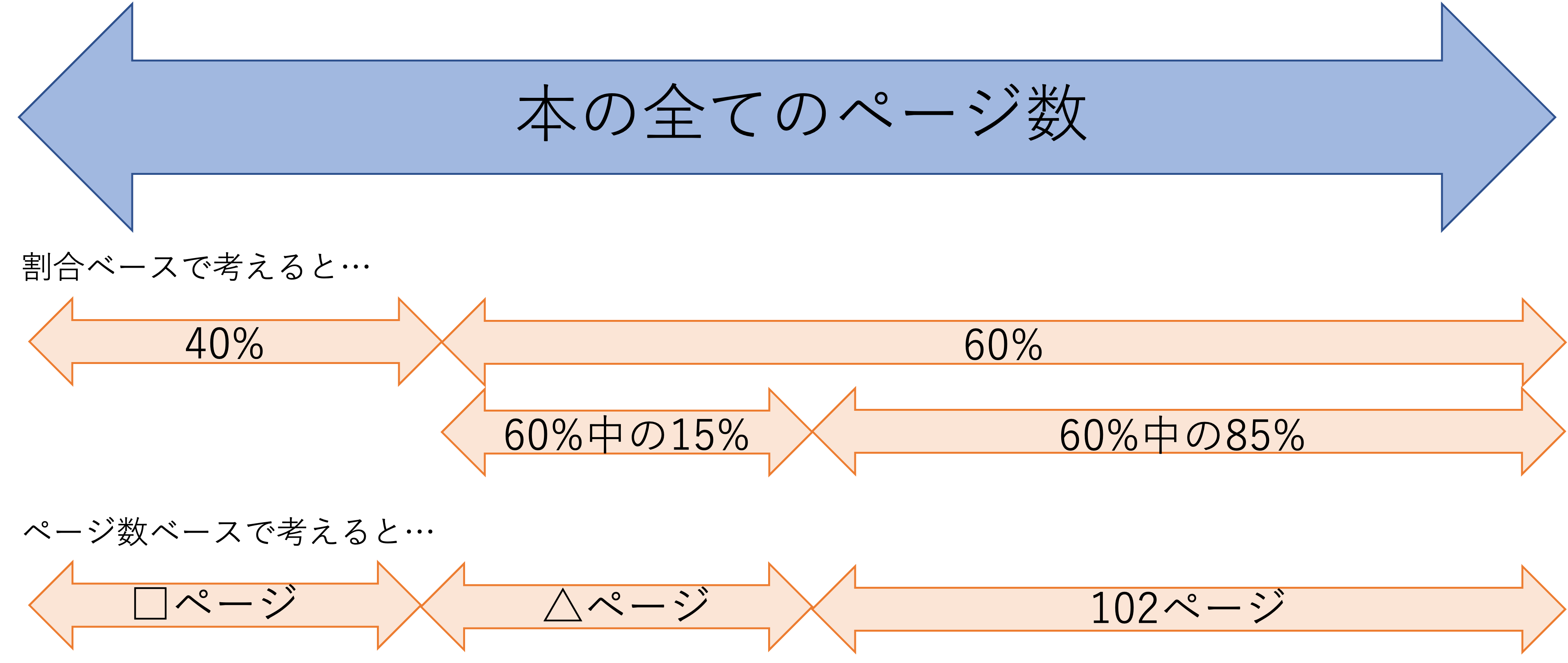
このような線分図を書く理由は,基準の違う数値の対比がしっかりとできるようになるからです。特に注目したいのが,50ページの部分です。この図から,2日目までに読んだ量を引いた残りである50ページというのが,割合で表すと初日に読んだ40%の余りである60%のうち,更に2日目に読んだ15%を引いた85%になることが一目瞭然です。その量はいったい何%になるでしょうか。計算してみると,
(1-0.4)×(1-0.15)=0.6×0.85=0.51
となるので,2日目までで読んだ量を引いた残りは全体の51%だということがわかりました。そしてその量が102ページだということは,比の関係から,
51%:102ページ=1%:2ページ
だと明らかになりました。そして1%が2ページだということは,全体つまり100%のページ数が200ページだという答えが求められますね。このように割合と数字といった2つの基準が相当する部分を計算して,全体の値を求めていくというのが還元算・相当算の攻略法になります。そしてこの攻略法を使う上で,線分図がとっても有効であるということをご理解いただければ幸いです。
今回ご紹介した解き方では,計算を簡単に進めるために□のある式を敢えて出しませんでしたが,難しい問題を早く解くとなると,やはり□を使った計算が必要になります。そのような問題の解説は上級編で行いますので,よければ読んでみてください。
まとめ
本記事ではこれまで還元算・相当算に関する内容の中級編として,式の組み立て方や文章の構造などについてお話ししていきました。最後に考えるコツや線分図の書き方をおさらいしておきましょう。
- 還元算・相当算は2つの基準があるかどうかで判断しよう!
- 2つの異なる基準を線分図で表し,どの部分が重なっているか考えよう!
今回ご紹介したのは還元算・相当算という限定された問題以外のどんな問題においても応用が利くような内容になっています。そのためおすすめ記事や参考文献を使いながら,テクニックとして身につけていきましょう。本記事が今後の学習のお役に立てば幸いです。

















