小学校の算数にはいくつかつまずきやすい単元がありますが, その中の1つに比の性質というものがあります。多くの小学生がここで苦戦してしまい,そのせいか中学受験でも頻繁に出題されます。そこで本記事では比の性質というものを簡単にまとめていくシリーズの後編として,応用問題の解き方を取り上げていきます。問題集形式で一緒に解きながら,比の性質を攻略していきましょう。
Contents
比の性質をおさらいしよう!
まずは前回の記事で取り扱った比の3つの性質を思い出しておきましょう。比とは,割合と同じように,あるモノとあるモノの比率を表したものです。1つの数を基準とする割合と違って,2つの数の大きさをそのまま関係として整理したものが比の正体になります。
この比に存在する3つの性質とは,分数に置き換えられる・かけたり割ったりして簡単にできる・かけ算で整理できる,ということでしたね。このように,比の形を変えたり簡単にしたりして問題を進めていく,というのが比の計算においてとっても重要なことです。今回引用する問題でもこれらの性質を使うことが多いでしょう。今回と前回の記事だけで3つの性質を覚えるのは難しいかもしれませんが,是非解きながら頭に入れる努力をしてみてください。

問題① 典型的な比の文章題!
それではここからは問題演習に移りましょう。実際に受験で登場した問題を引用していますので,解いてみる価値は大いにあるかと考えられますが,何もちゃんと解かなくとも記事を読んで理解するだけでも得点力向上に役立つでしょう。「どうやって解くのかな」と考えながら読んだり解いたりしてみてください。
長さが80cmの針金を折りまげてたてとよこの長さの比が3:2になるように,長方形を作りたい。たての長さを何cmにすればよいですか。
(文教大学附属中学校(2013),一部改題)
解説①
それでは解説に移ります。といっても,このくらいの水準の問題は小学校の授業でも登場するので,もしかしたらサクッと解いてしまった人もいるかもしれませんね。この問題では,長方形のたての長さとよこの長さが3:2になる,というところで比が登場していました。今回はたての長さが求められているので,たての長さを□cmとおきましょう。このように分からないところを□にして考える,ということが算数では大切です。
次に今回の問題の条件について眺めていきましょう。今回は針金を長方形にする,という問題でした。これをひも解くと,針金はたて―よこ―たて―よこの4つの分割されることが分かります。そしてこの分け方において長方形のどの部分に相当するかを考えると,たてとたて・よことよこが等しいことから,針金を3:2で分けるということと同じ意味になります。このことから,たての長さに使う針金とよこの長さに使う針金の比は3:2になり,□cmの中身はその半分になるというわけです。
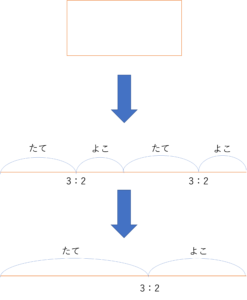
そして3:2で分けられるということは,たての長さに使う部分の長さは全体の\(\frac{3}{5}\)になるというわけです。従って答えは次のようにして求められます。
\(□=80\times\frac{3}{5}\div2\)
\(□=24\)
このことからたての長さは24cmとなります。今回の問題では比は分数で置き換えられるという性質を使いましたが,かけ算で整理する方法も使えそうですね。色々な解き方があるかと思うので,別の方法でも答えが出せないか試してみるのもいいでしょう。
A.24cm
問題② 計算が煩雑な比の文章題!
続いてはちょっと計算がややこしい問題をご紹介します。こちらも3つの性質を理解していれば無事に解けますので,途中の□を使った式の処理に注意して進めてみましょう。
姉と妹の所持金の比は5:3でした。姉は1冊400円の本を2冊買い,妹はおじいちゃんから500円のおこづかいをもらったので,所持金の比が6:5になりました。姉の初めの所持金は何円ですか。
(日本大学第二中学校(2010),一部改題)
解説②
それでは解説に移ります。この問題でも,まずは求められている姉の初めの所持金を□円とすることから始めていきましょう。そしてこの□円を元に,妹の所持金・姉が本を買った後の所持金などを考え,比の形でつなぎ合わせていくと考えていきます。そうすると初めに妹の初めの所持金が分かりそうですね。初めは姉と妹の所持金の比が5:3だったことから,妹の所持金は次のように表せます。このとき,かけ算を使って比を整理するという性質が使われていることがポイントです。
□:妹の所持金=5:3
5×妹の所持金=3×□
妹の所持金=\(\frac{3}{5}\times\)□(円)
ということで,姉と妹が初めに持っていた所持金が分かりました。ここから姉が本を買った・妹がお金をもらった後の所持金のことを考えていきます。まだ答えがどのようになるか予想はつかないかもしれませんが,算数で大切なことは答えを予想する前に手を動かすことです。計算を進めれば次第に答えに辿り着けるでしょう。
さて姉が本を買った後の所持金ですが,こちらは400円×2=800円お金を払っているので□-800(円)となります。他方妹の所持金が,おこづかいの分500円増えるので\(\frac{3}{5}\times+500\)円となります。そして2人の所持金の比が6:5と言われているので,次のような式が成立します。このとき,かっこのあるかけ算の計算方法に注意して資格の値を求めることが重要です。
□-500:\(\frac{3}{5}\times□+500\)=6:5
\((\frac{3}{5}\times□+500)\times6=5\times(□-800)\)
\(\frac{18}{5}\times□+3000=5\times□-4000\)
\(\frac{18}{5}\times□+3000\times6=5\times□-4000\)
\(\frac{3}{5}\times□=1000\)
□=600
このように複雑な計算をこなすと600円という答えが出てきます。複雑といっても,中学受験レベルだとこのくらいの水準の分数やかけ算の処理は頻繁に出てくるのですが,比とセットになると途端に難しく感じやすいです。ぜひ対策してみてください。
A.600円
問題③ 2つの比をつなぎ合わせて考える文章題!
それでは最後に2つの比をうまくつなぎ合わせる問題です。
次の□にあてはまる数を求めなさい。
AさんとBさんの所持金の比は1:2で,BさんとCさんの所持金の比は3:4です。Cさんの所持金が560円だとすると,3人の所持金の合計金額は□円です。
(西武台新座中学校(2019),一部改題)
解説③
この問題も,上の二つと同様に解説を行っていきます。この問題では所持金の合計金額が問われていますが,今回はAさんの所持金を□円と設定して問題を読み進めてみましょう。ここで合計金額を□としないのは,□で表しても式に使えなさそうだからですね。
ということでまずは順番にBさんの所持金を□で表していきましょう。AさんとBさんの所持金の比が1:2であることから,Bさんの所持金は,
□:Bさんの所持金=1:2
Bさんの所持金=2×□
となります。この式ではかけ算によって比の等式を簡単にできるという性質が使われています。そしてこの式を元に,今度はBさんとCさんの所持金の関係を式で表してみましょう。Bさんの所持金とCさんの所持金は3:4であり,Cさんの所持金は560円だったので,次のように整理できます。
Bさんの所持金:Cさんの所持金=3:4
Bさんの所持金:560=3:4
Bさんの所持金:560=3×140:4×140
Bさんの所持金:560=420:560
この式から,Bさんの所持金は420円だと判断できます。ここでは比はかけたり割ったりして形を変えられるという性質を使っています。そしてAさんの所持金である□円は,Bさんの所持金である2×□円の半分だったので,Aさんの所持金は210円だと計算できます。このことから所持金の合計金額は210+420+560=1190円になります。
A.1190円
いかがでしたでしょうか。2つの比をつなげると言うと難しそうに聞こえますが,実は基本的な計算を組み合わせているだけで意外とサクッと解けてしまったりします。諦めずに解いていきましょう。
まとめ……の前に
登録6000人以上!
本サイト、中学受験ナビの監修も務めている『開成番長』こと繁田和貴が執筆する完全無料のメールマガジンでは、主に中学受験生のお子さんをお持ちの方へ向けた様々なお役立ち情報を配信中!
さらに今なら登録者にはもれなく「開成番長・繁田監修 中学受験必勝の5箇条PDF」をプレゼント!
登録及び登録解除も簡単ですので、お気軽にご登録ください。

まとめ
今回は比の性質について扱う記事の第二弾として,受験に登場した問題を引用しながら攻略法をご紹介していくというものでした。意外と応用問題は手強くない!ということが伝わっていたら幸いです。比の性質をはじめ,中学受験の算数を乗り切る上で必要な学力やセンスは勉強量でいくらでも身につけられます。よろしければおすすめ記事や参考書なども使いながら,ともに頑張っていきましょう。
(ライター:大舘)
















