今回の記事は場合の数・確率の攻略法!【応用編その1】の続きの記事になります。本記事でも場合の数・確率といった範囲から出題された入試問題を2つほどご紹介し,同じような問題が本番で出されたときどのように対処していけばいいのか,という攻略法やポイントをご説明いたします。
ただ基礎的な知識が身に付いていない場合,少しわかりづらい箇所もあると思います。そのようなときはおすすめ記事の欄にある【基礎編】や【標準編】を参考にしてみてください。
Contents
問題を解いてみよう①
それでは早速ですが問題を解いていきましょう。樹形図やかけ算のテクニックを思い出しながら,丁寧に計算していきましょう。
1,2,3,4のカードが1枚ずつあります。よく混ぜて1枚ずつ計3枚引きます。1番目に引いたカードの数と2番目に引いたカードの数をかけて,その結果に3番目に引いたカードの数をたす操作をします。このとき,次の各問いに答えなさい。
(1)この操作の計算結果のうち,最大の数はいくつですか。
(2)この操作の計算結果は,全部で何通りですか。
(3)この操作の計算結果が7になるとき,カードの引き方は全部で何通りありますか。
(山手学院中学校(2019),一部改題)
解説①(1)
ではここからは解説に移ります。いまいち解き方がわからなかった,という人は解説を見ながらでもいいので,一緒に樹形図を作りながら学んでいきましょう。
まず初めに問題文を簡単に理解するところから始めましょう。かける・たす,という操作がたくさん出てきていますが,この問題では要するに3枚の数字の組み合わせが求められているだけなのです。したがって具体的な計算を始めていく前に,樹形図を作ってカードの並べ方が合計で何通りあるのかを計算していきます。場合の数の問題ではこのように,先に樹形図を書いてしまうと簡単になるパターンが多いです。覚えておきましょう。次の図が本問題で想定されている樹形図になります。
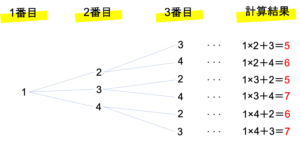
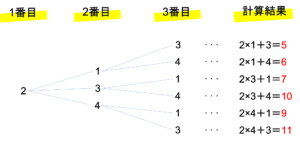
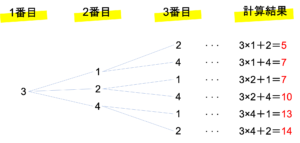
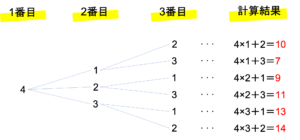
左側の樹形図がカードの組み合わせを,左側の式が条件に沿って計算した結果を表しています。このように樹形図を作ったときに,同時に計算の結果や○×といったマークをつけておくと,その後の計算が早くなります。以下では図を元に(1)・(2)・(3)の設問を解いていくことにします。
では(1)の答えを考えていきましょう。今回聞かれていたのは,計算結果のうち最大の数になります。上の樹形図に書かれている計算結果の欄を見ると,14が最も大きいことがわかりますね。したがってこの問題の答えは14となります。
解説①(2)
次に同じように樹形図を見ながら(2)の問題を解いていくことにしましょう。今回聞かれているのは計算結果が何通りとなるかです。したがって計算結果の欄を見て比較していけばいいのですが,ここで注意しなければならないのは計算結果の数=カードの組み合わせの数ではないということです。
例えば上の樹形図の中の,1-2-3というカードの並びと1-3-2というカードの並びに注目しましょう。この2つはカードの並べ方としては全くの別物です。しかし計算結果は両方とも5になりますよね。このような数字の並びの違いを考慮せずに式で導かれた値の数を考えていく,というのが今回の条件になります。間違えて並び方の数を数えてしまわないように,問題文をよく読んで何が問われているかを正確に見極めましょう。
では計算結果は果たして何通り存在するのでしょうか。数え上げていくと以下のようになります。
4,5,6,7,9,10,11,13,14
よって計算結果は合計9通り存在することがわかりますので,答えは9通りとなります。
解説①(3)
最後に(3)の答えを導き,問題を締めくくりましょう。計算結果が7通りとなるときのカードの引き方を考えていきます。今回はカードの引き方を1番目・2番目・3番目と区別しているため,数字の並びをそのまま数え上げていけばいいですが,問題によってはカードを引く順番が関係ない場合もありますので,「並べる」と「選ぶ」の違いには常に気をつけていきましょう。
さて,計算結果が7になるときのカードの引き方ですが,樹形図を見ると次の並びが当てはまることがわかります。
1-3-4,1-4-3,2-3-1,3-1-4,3-2-1,4-1-3
このことから答えは6通りとなります。
A.(1)14,(2)9通り,(3)6通り
問題①のまとめ
いかがでしたでしょうか。今回の問題では樹形図を正しく書けたか書けなかったか,問題文の指示を正しく汲み取れたかが重要な点でした。改めて解答時の細かいポイントをおさらいしておきましょう。
- 設問に取り組む前に問題文を簡単に理解することから始めよう!
- 樹形図を作ったときに,同時に計算の結果や○×といったマークをつけておこう!
- 「並べる」か「選ぶ」か・尋ねられているものは何かには常に気をつけよう!
このようなポイントは他のどんな問題を解くときでも役に立つものなので,常に意識できるようになると望ましいです。さっそく次の2問目を解くときに意識してみましょう。
問題を解いてみよう②
それでは2問目に移ります。先ほどより問題文が長いため,じっくりと読んで内容を整理することから始めていきましょう。
生徒から1個ずつ集めたプレゼントを先生が生徒に分けることにしました。次の空欄に当てはまる数を答えなさい。
(1)A,B,Cの3人から集めたプレゼントを先生が分けます。
(ア)3人とも自分のプレゼントを受け取るとき,その分け方は1通りあります。
(イ)3人とも他の人のプレゼントを受け取るとき,その分け方は2通りあります。
(ウ)3人のうち,1人だけが自分のプレゼントを受け取るとき,その分け方は ①通り あります。
その後,遅れてDがプレゼントを持ってきました。ここから3人のうち, 誰か1人とプレゼントを交換することで4人とも他の人のプレゼントを受け取る分け方を考えます。
(ア)の場合は,誰と交換しても分けられません。
(イ)の場合は,A,B,Cの誰か一人と交換すれば,分けられます。
(ウ)の場合は,A,B,Cのうち,自分のプレゼントを受け取った人と交換すれば,分けられます。
以上のことから,四人とも他の人のプレゼントを受け取る分け方は ②通り あります。
(2)4人の生徒のプレゼントを先生が分けるとき,4人のうち1人だけが自分のプレゼントを受け取る分け方は ③通り あります。
(3)5人の生徒のプレゼントを先生が分けるとき,5人とも他の人のプレゼントを受け取る分け方は ④通り あります。
(早稲田中学校(2020),一部改題)
解説②(1)
それではここからは問題の解説に移ります。この問題は(1)・(2)・(3)と移るたびにプレゼント交換に参加する生徒の数が増えていきます。したがって当然のことながら,後半の問題の方が難しかったかと思われます。しかし樹形図を書いて答えを導き出すという解き方は変わりませんので,落ち着いて解いていきましょう。
この問題での樹形図は誰がどのプレゼントを受け取るかで書くといいでしょう。自分のを受け取るか他人のを受け取るかでパターンが別れていましたが,まずは1問目と同じ要領で樹形図を書いていきます。このときプレゼントは1個ずつしかないことに注意して書いていくと,次の図が出来上がります。
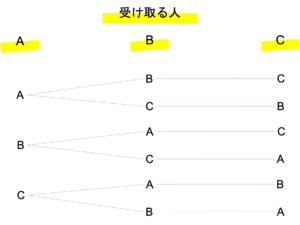
このことから,プレゼントの分け方は合計6通りあることがわかりました。先ほどの問題でも同じような説明を行いましたが,このような場合の数の問題は,設問に取り組む前に樹形図を書くことで効率的に解くことができます。
ではこの樹形図を見ながら,3人とも自分のプレゼントを受け取る(ア)・3人とも他の人のプレゼントを受け取る(イ)・1人だけ自分のプレゼントを受け取る(ウ)に分けていきます。このときわかりやすいように,自分のプレゼントを受け取っている場合には下のような印をつけていきましょう。
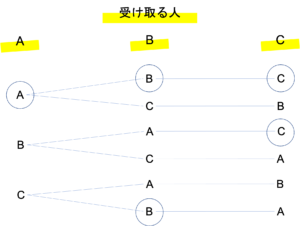
このことから問題文の通り(ア)は1通り・(イ)は2通りであることがわかりました。このとき(ウ)に該当するのは,
A-C-B,B-A-C,C-B-A
の3通りだとわかりますので,答えは3通りとなります。なお今回は空欄に当てはまる数が問われているので数字の3だけを答えればいい,ということに気をつけましょう。
次にDさんが来たときのことを考えていきましょう。問題文では(ア)の場合・(イ)の場合・(ウ)の場合を考えていますので,それに従っていけばいいですが,(ア)の場合は分けられないと既に結論づけられているので,(イ)と(ウ)のときを考えます。このように省略できるところがないかを問題文から読み取る力も重要です。
まずは(イ)からです。全員が他の人からのプレゼントを持っていた場合,誰がDさんとプレゼントを交換しても成立することが問題文からわかります。いまA・B・Cの3人について,(イ)に当てはまる場合は2通り存在し,それぞれDがAと交換する場合・Bと交換する場合・Cと交換する場合の3通りが考えられるため,2×3=6通りとなります。
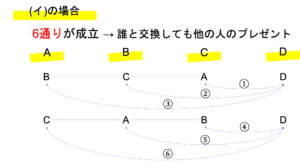
次に(ウ)の場合について考えていきましょう。(ウ)の場合,1人だけ自分のプレゼントを受け取っています。したがってDさんが参加した後に全員が他の人からのプレゼントを持っている状態にするには,これも問題文の指示通り自分のものを持っている人とDさんとが交換すればいいことがわかります。
いま(ウ)の場合は,自分のプレゼントを持っているのがAさんのとき・Bさんのとき・Cさんのときの計3通り存在します。これらの場合についてDさんはそれぞれAさん・Bさん・Cさんと交換するしかないので,3×1=3通りとなります。

よって(イ)の場合で6通り・(ウ)の場合で3通りということがわかったため,答えは6+3=9通りとなります。この手の問題では,①の答えに引っ張られ,(ア)以外が当てはまるから6-1=5通りだ!と考えてしまいがちなのですが,問題文をきちんと読んで丁寧に解いていきましょう。
解説②(2)
では次に(2)の問題に移ります。4人がプレゼントを交換するときのことが尋ねられていますね。自分のプレゼントを受け取る人を固定する解き方もありますが,ここではやはり樹形図を使って解いていくことにしましょう。4人をA・B・C・Dとし,図を作っていきます。このときも(1)と同じように,自分のプレゼントを受け取っている場合には○印をつけていきます。
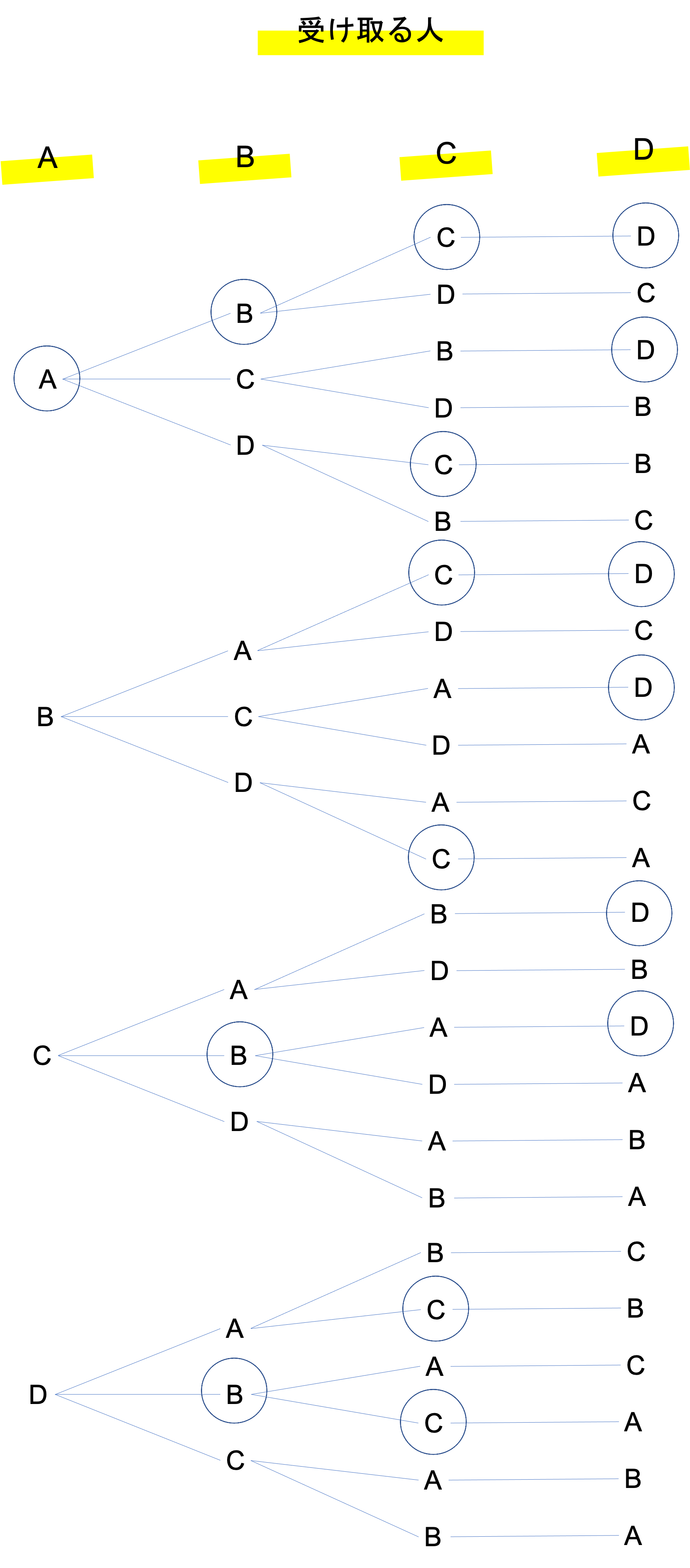
この樹形図を見ると,全員が自分のプレゼントを持っていたり,何人かが自分のプレゼントを持っていたりと,様々なパターンが見られることがわかります。このうち1人だけが自分のプレゼントを受け取る分け方はいくつあるかを考えていくと,
ACDB,ADBC,BCAD,BDCA,CABD,CBDA,DACB,DBAC
の8つが当てはまるものだとわかります。したがって答えは8通りとなります。
解説②(3)
では最後に5人になったときの場合の数について考えていきましょう。5人をA・B・C・D・Eとし,5人とも他の人のプレゼントを受け取る場合を(2)と同様の手順で樹形図を書いて求めていってもいいですが,5人分の樹形図をなると手間がかかりそうです。
ここで,この問題を解くために余事象の考え方を用いていきましょう。「5人とも他の人のプレゼントを受け取る」ということの余事象は,「5人のうち少なくとも1人は自分のプレゼントを受け取る」になります。
つまり自分のプレゼントを受け取るのが1人の場合・2人の場合・3人の場合・4人の場合・5人の場合を考えて,全部の場合から引くことで計算できそうです。ここで全ての場合の数は5×4×3×2×1=120なので120通りです。
ではまず1人が自分のプレゼントを受け取る場合を考えます。自分のプレゼントを受け取る人がまず5通り存在します。その5人のうち4人が他人のプレゼントを受け取ればいいですね。例えばAが自分のものを受け取るとすると,B・C・D・Eが他の人のプレゼントを受け取ればいいわけです。
ここでこの4 人については自分のプレゼントを受け取ってはならないので,BはCかDかEのプレゼントを受け取らなければいけません。続いてCは,BがCのプレゼントを受け取っていた場合はB・D・Eのどれかを,BがDかEのプレゼントを受け取っていた場合はその残りとBのどちらかを受け取らなければなりません。このような選択肢による差を考えていくと次のような樹形図が書けます。
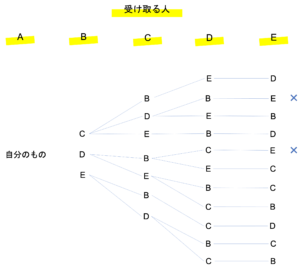
したがって該当するのは9通りだとわかりました。これと同じことが自分のものを受け取るのがBのとき・Cのとき・Dのとき・Eのときでも言えますので,特定の1人の選び方5通り×残り4人の選び方9通り=45通りとなります。
次に2人が自分のプレゼントを受け取る場合を考えていきましょう。まず5人の中から自分のプレゼントを受け取る2人の組み合わせを考えましょう。組み合わせは,
A&B,A&C,A&D,A&E,B&C,B&D,B&E,C&D,C&E,D&E
の10通りが考えられます。では2人のプレゼントを固定して,残った3人全員に他の人のプレゼントを配る分け方を樹形図で考えましょう。
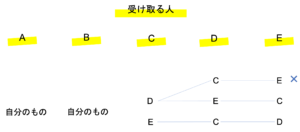
したがって2人が自分のプレゼントを受け取るとき,残りの3人への配り方は2通りとわかりました。いま上で,この2人の選び方は10通りと計算しているので,当てはまる場合の数は2×10=20通りとなります。
続けて3人が自分のプレゼントを受け取る場合を計算します。2人のときと同様に,まずは自分のプレゼントを受け取る3人の組み合わせを数えましょう。その組み合わせは,
A&B&C,A&B&D,A&B&D,A&C&D,A&C&E
A&D&E,B&C&D,B&C&E,B&D&E,C&D&E
の10通りだとわかります。そしてまた同じように,残った2人へのプレゼントの分け方を考えましょう。今回は例としてA・B・Cが自分のプレゼントを受け取るとします。
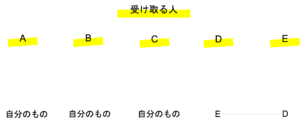
上の図から2人へのプレゼントの分け方は1通りしかないことがわかります。このことから,3人の組み合わせと2人への分け方が求められたので,当てはまる場合の数は10×1=10通りとわかります。
それでは4人が自分のプレゼントを受け取る場合を考えましょう。しかし4人だけが自分のもので1人だけが他の人のものを受け取る,という分け方は存在しません。4人が自分のプレゼントを持っているのであれば,残った1人と残りのプレゼントを持ってきた人は一致します。このことから4人が自分のプレゼントを受け取る場合は0通りです。
では最後に5人全員が自分のプレゼントを受け取る場合を考えていきましょう。これはA・B・C・D・EがそれぞれA・B・C・D・Eのプレゼントを受け取るという1通りしかありません。
これらをまとめると,今回の5人とも他の人のプレゼントを受け取る分け方の余事象は45+20+10+1=76通りとわかります。このことから全員が他の人のものを受け取る場合の数は,120-76=44通りとなり,答えは44通りと求められます。
A.①3,②9,③8,④44
問題②のまとめ
以上が2問目の解説になります。なかなか手応えのある問題だったのではないでしょうか。このような難しい問題でも,基礎的な樹形図というテクニックだったり,余事象という観点だったりは変わらず役に立ちます。今回で重要となったポイントは次の通りです。
- 設問に取り組む前にまず樹形図を書こう!
- 問題文をよく読んで,問われているものを正確に理解しよう!
- 手間がかかりそうな問題では余事象の考え方を活かそう!
終わりに
以上で【応用編その2】の記事は終わりとなります。2問しか引用しなかったとは言え,どちらも難関校からの出題であり,難しいと感じた人が多かったと思います。しかし演習を積み重ねることで,次第に慣れていくでしょう。実力がついた時に再チャレンジしてみるのもいいかもしれません。本記事が学習の手助けとなれば幸いです。
おすすめ記事
- ”並べる”と”選ぶ”の計算方法の違い
- 場合の数・確率の攻略!【基礎編】
- 「じゃないほう」の場合を考えよう!場合の数・確率の分野の攻略法【標準編】
- 入試問題に挑戦してみよう!場合の数・確率の分野の攻略法【応用編その1】
参考
- 山手学院中学校・高等学校,最終アクセス:2021/02/28
- 早稲田中学校・高等学校,最終アクセス:2021/02/28