今回の記事では整数の規則について説明していきます。私たちは整数というものを日常的に使っていますが,その仕組みについて説明されることは多くありません。特に今回紹介する倍数の法則については,小さい数字は取り上げられやすいものの,それ以外の数にはなかなか焦点が当てられません。したがってこの記事では,合計8種類の整数について,その倍数がどんな数になるのか説明していきます。
Contents
整数・倍数とは?
本題に入る前に,ここでは整数や倍数といったものがどういった数を指すのかについて説明していきます。まずは整数という概念についての解説です。改めて説明するまでもないでしょうが,整数とは0を基準に1を足して作ることのできる数のことを指します。例えばパッと思いつく整数として1や2や3が挙げられますが,これらは0+1,0+1+1,0+1+1+1,といったように表されますよね。逆に整数でない数を考えてみると,0.1・0.2といった小数や,2分の1・3分の1といった分数が存在するわけですが,これらの数は1だけを足すのでは作ることができないですよね。例えば0.1は1を10で割らないと,2分の1は1を2で割らないといけないので,整数にはカウントされないということです。
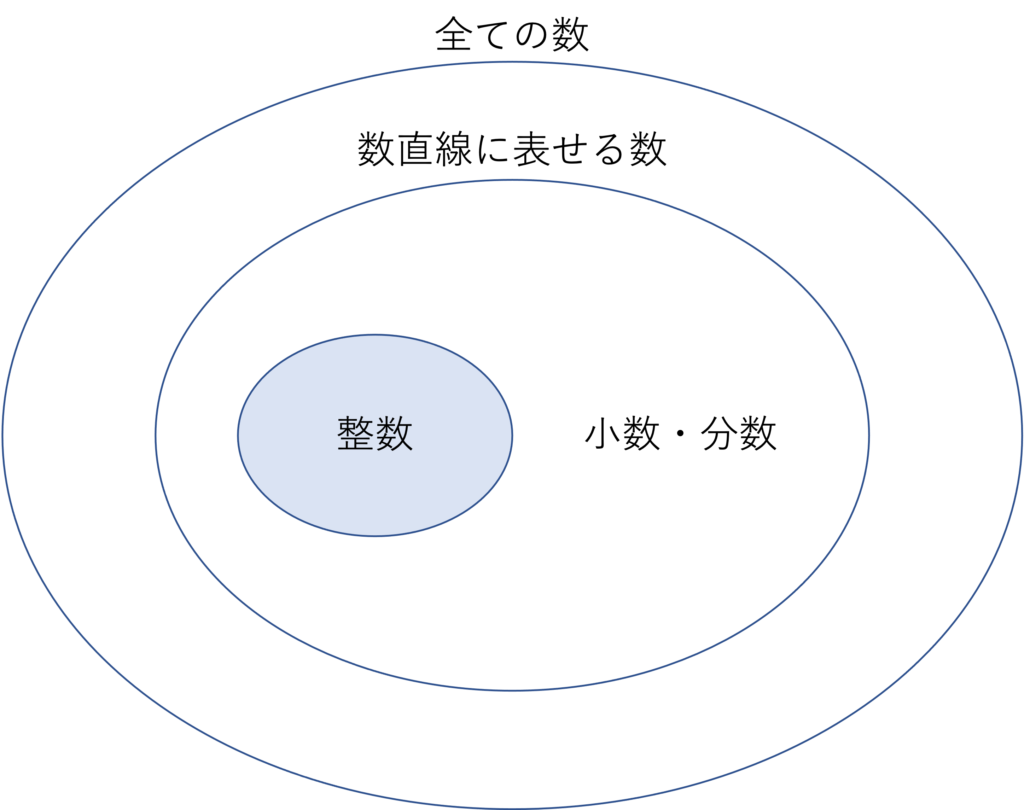
では倍数とはどのような数を指すのでしょうか。倍数とはある数を整数でかけ算したときの数を指します。例えば4という数を考えたとき,4は1×4なので1の倍数と考えることができます。また同様に4は2×2でも表されるので2の倍数,4×1でも表されるので4の倍数と考えることもできます。また0.5×8のように捉えるのであれば,0.5の倍数とみなすこともできますね。このようにすべての数は色々な数の倍数として捉えることができるのですが,一部の数は1とその数自身の倍数でしかないものもあります。その例としては2や3や5が挙げられますが,このような数のことは素数と呼びます。今回扱うのは倍数のみについてですが,併せて覚えておきましょう。
2の倍数の性質
それではここからは受験に登場しやすい倍数の性質について,〇〇の倍数は△△な数になるといった形で解説していきます。まずは2の倍数についてです。性質を簡単に述べるとすべての2の倍数,つまり偶数はその数の一の位が2の倍数になります。この法則は一番小さい2の倍数である2に,2を足していくと見出すことができます。
2を基準に2を順番に足していくと,2,4,6,8,10,12,14,……となりますね。この整数の並びから一の位のみを取り出すと,2,4,6,8,0,2,4……となり,0から8までの5つの偶数が循環していくことが分かります。このことから末尾が偶数であれば,その整数は2の倍数になるという法則が説明できるわけです。このように末尾に注目するのは,十の位より上の数と一の位とで整数を分けると,10の倍数+1桁の整数と捉えることができるからです。このとき10の倍数は2の倍数でもあるので,一の位に残った1桁の整数が偶数であるかどうかでその数が2の倍数であるかどうかも決まるということですね。
3の倍数の性質
続いては3の倍数についてです。3の倍数にはその整数のすべての位の数を足したときに3の倍数ができあがるという法則があります。例えば3の倍数の12や15や21は,それぞれくらいの数を足すと1+2=3,1+5=6,2+1=3とすべて3の倍数になりますね。これはどんなに大きい数でも言えることであり,3×2022=6066という大きな数でも6+0+6+6=18と,位を順番に足せば3の倍数になるのです。
その理由は,3の倍数である整数をそれぞれの位で切り分けて,1が○個,10が△個,100が□個,……と捉えると分かりやすくなります。例として123という整数があるとして,これは100が1つ・10が2つ・1が3つ,つまり100+20+3とみなすことができますよね。この3つに切り分けた数字をそれぞれ3で割ってみましょう。すると100を3で割った余りが1,20を3で割った余りが2,3を3で割った余りが0になり,この余りを全て足し合わせると3になります。しかし3は3で割り切れるので,無事余りまで3で割り切れることになり,整数全体が3で割り切れると言えるわけです。
ここで,余りとして足し合わせた1・2という2つの数字に注目すると,最初に例として挙げた123の百の位と十の位の数と同じになっていることが分かりますよね。そして一の位である3は当然3の倍数ですので,1・2の部分の和が3の倍数であれば,3を足しても3の倍数のままになります。この関係から3の倍数を見分けるためにそれぞれの位の数を足すというテクニックを使うのであり,その合計が3で割り切れるというのは整数を3で割ったときの余りが発生しないことと同じことを指すので,判定法として有効であると言えるのです。
4の倍数の性質
ここからは4の倍数の性質を解説していきます。4の倍数は,下2桁が4の倍数かどうかで判断することができます。このことは2の倍数と同じように,4の倍数を順番に並べていったときに分かりやすくなります。4の倍数を順番に並べると4,8,16,……となり,これを繰り返すと92,96,100,104,108,……と100を境に下2桁が循環していくことが発見できますね。そのため下2桁,つまり十の位と一の位に注目したとき,その数字が4の倍数であれば整数そのものも4の倍数だと言えるのです。
この性質が成立する理由,は整数を百の位以上と十の位以下で分けると明らかになります。このように切り離したとき,整数は100の倍数+2桁の整数という形で捉えることができますが,100は4の倍数ですので,2桁の整数の部分が4の倍数であれば整数自体も4の倍数となります。このようなカラクリで法則は成り立っているのです。
5の倍数の性質
次は5の倍数の性質について説明していきます。5の倍数には末尾が0か5になるという性質があります。その理由は2の倍数を見て行ったときと同様の手順で考えることができます。5の倍数を順番に考えていくと,5,10,15,20,……となりますが,このときの一の位に注目すると5,0,5,0,……と2つの数を行き来していることが分かります。そのため末尾が0か5であれば5の倍数であると言えるわけです。
このような法則が成り立つ理由も,2の倍数と同じように考えることができます。2の倍数のときは十の位以上と一の位で数を分けましたが,ここでも同じように十の位より上の数と一の位とで整数を分け,10の倍数+1桁の整数と数を捉えていきましょう。そうすると10の倍数は5の倍数でもあることから,1桁の整数の部分が5の倍数である0か5なら,その整数は5の倍数であるという結論が導けるのです。

6の倍数の性質
続いて6の倍数の性質について考えていきましょう。そもそも6という数字は,2×3というかけ算で成り立っていますね。そのため6の倍数は2の倍数と3の倍数の性質を合わせ持つ,つまり末尾が2の倍数でありすべての位の数を足すと3の倍数になる,という性質があります。例えば6×2022=12132という数字があるとして,この数字は6に2022をかけたので確実に6の倍数のうちの1つです。この12132という数の一の位に着目すると2という偶数になっているので,12132は2の倍数です。これと同時にすべての位の数を足し合わせると,1+2+1+3+2=9=3×3と3の倍数になっていることが分かります。それゆえ,この12132という数で見たように,6の倍数には2の倍数の法則と3の倍数の法則が当てはまるという説明が成立するのです。
なおここでは6の倍数を6=2×3というかけ算に直し,その中で使われている数の性質が当てはまるという解説をしましたが,これは他の素数以外の数の倍数についても当てはまります。例えば10の倍数であれば10=2×5であることから2の倍数と5の倍数の性質の両方を持っていますし,12の倍数であれば12=3×4なので3の倍数と4の倍数の性質の両方を持っています。そのため大きな数の倍数に関する問題が出た場合,その数がどのようなかけ算で表されるかを先に検討して,そのかけ算で使われたすべての数の性質を使っていくといいでしょう。
7の倍数の性質
次に7の倍数の性質についてご紹介していきます。7の倍数の見分け方は,まず整数を3桁ごとに区切ることから始まります。こうしてできた3桁以下の数字のグループを右から足す→引く→足す→……と繰り返すときにできる数が7の倍数であるとき,その整数は7の倍数となります。例として7×12345678=86419746という数について考えていきましょう。この数を3桁ごとに区切ると86と419と746の3つの数に分解できます。そして上で説明した手順通りこれらの数字を計算式に落とし込むと,746-419+86という式が出来上がります。この計算結果は413になるのですが,413という数は7×59で表されるので,7の倍数です。したがって86419746も7の倍数だ,というふうに考えていくのが7の倍数の見分け方になります。この法則は説明に中学生の数学の内容を必要とするので,誤解を避けるためにも深くは解説いたしませんが,もし「なぜそうなるの?」と疑問に思う方がいましたらご自身で検索をかけていただけますと幸いです。
9の倍数の性質
ここからは9の倍数の性質について説明していきます。9の倍数の性質は3の倍数のところで使った考え方と同じように,すなわちそれぞれの位の数を使って説明することができます。その性質を簡単に説明すると,それぞれの位の数を全部足した合計が9の倍数になるという性質が9の倍数にはあるのです。例えば9×2022=18198という整数があったとして,この数字のそれぞれの位の数を抜き出すと1・8・1・9・8となりますが,これらを全て足した計算結果は1+8+1+9+8=27です。ここで27は9×3=27であることから9の倍数の1つです。このようにすべての位の数を足したときに9の倍数になる数字が9の倍数だと言えるわけですね。
この性質が成立することも,3の倍数と同じ手順で証明することができます。先ほど例として挙げた18198という整数をそれぞれの位で分解して,10000+8000+100+90+8と捉え,これらの数字をそれぞれ9で割り算してみましょう。すると10000を9で割った余りが1,8000を9で割った余りが8,100を9で割った余りが1,90を9で割った余りが0,8を9で割った余りが8であり,これらを足し合わせると1+8+1+0+8=18となります。しかし18は9で割り切れるので,余りまで9で割り切れることになります。
ここで足し算の中身と整数の形を照らし合わせると,1・8・1・8という数字が18198という数の十の位以外の数字と共通していることが分かります。そして十の位である9は言うまでもなく9の倍数なので,9の倍数以外の数の和が9の倍数であれば,そこに9の倍数を足しても9の倍数になるという関係から,9の倍数を見分けるために全ての位の和を足し合わせるというテクニックが使えるのです。
11の倍数の性質
それでは最後に11の倍数の性質について触れて本記事を締めくくります。11の倍数の性質としては,見分けたい整数の位を一つ飛ばしに足していったときに出来る2つの数字が11の倍数の分だけ離れているというものが挙げられます。これも9の倍数に引き続き分かりづらい判別方法ですが,例として11×2022=22242という数字について考えてみましょう。この数字をそれぞれの位で分け1つ飛ばしで取り上げていくと,2・2・2というグループと2・4というグループを作ることができます。これらをグループごとに足し合わせるとどちらも6になりますね。そのため2つの差は0になるわけですが,この0という数字は11×0=0ということで11の倍数と言えます。そのため22242は11の倍数だと言うことができるのですが,このような手順で考えていくと,ある整数が11の倍数かどうか判断することができるというわけです。
この仕組みが成り立つ理由も,7の倍数と同じように中学校レベルの数学を使わないと説明しきれない点があります。そのため初めて整数について触れる人は特に頭の中がこんがらがりやすいので,7の倍数同様に説明は割愛しますが,もし興味がある人はご自分で調べてみてください。

終わりに
今回の記事では整数の性質に焦点を当て,とりわけ整数が何の倍数になっているかを判別する方法についてご紹介していきました。整数の性質は受験でも頻繁に出題される範囲ですし,直接聞かれなくとも,計算の中でこれらの情報を使うことで簡単に解くことができるといった問題も一定数存在します。そのため完璧に頭の中に入れるだけでなく,習慣として知識を定着させておきましょう。本記事が今後の学習のお役に立てば幸いです。
(ライター:大舘)
おすすめ記事
- ケアレスミスを減らし計算スピードを上げるテクニック!インド式かけ算とは
- 整数の基礎をわかりやすくご紹介!整数問題を得意にしよう!!(練習問題付き!)
- 入試問題3選を解きながら解答の方法を身につけよう!虫食い算【応用編】


















