今回は還元算・相当算についてのお話です。「還元算・相当算って何?」と思う人もいるかもしれませんが、こちらは中学受験でよく出題される文章題の1つです。詳しい説明は記事の中で行っています。いまいちピンと来てない人でもわかりやすいように記事を作っておりますので、よければ一読してみて下さい。
Contents
還元算・相当算とは?
まずは還元算・相当算とは何か、ということについて説明していきます。これは受験算数で典型的な文章題の一つなのですが、そもそも還元・相当という言葉が難しいので、一体どんなものなのだろうと思う人が多いことでしょう。そのため、まずは言葉で説明するよりも例題を見ることで、「これが還元算・相当算というものなのか!」という感覚を掴んでいただけますと幸いです。
38÷(89-70)×(□+8)=104
{□÷(5+60)}×4=60
いま上で取り上げた2つの問題のように、□が含まれる計算が還元算・相当算のことを意味します。厳密に言えばこの例題はただの式でしかなく、このような□が含まれる式を組み立てる必要がある文章題のことが還元算、そしてそのうち特に割合が関係するものを相当算というのですが、ここでは大雑把に還元算・相当算とは□を使う計算のことだ、と覚えてしまうといいでしょう。
解き方を覚えよう!
それでは還元算・相当算とは何かを理解してもらえたところで、□を使った計算はどうやって解けばいいのかということ解説していきます。今回は文章題の抑え方ではなく、まずは答えの求め方・式の変形の仕方などについて、初めての人でもわかりやすいように解説していきます。もしこの辺りの計算の基本はバッチリだという方がいましたら、次の中級編の記事に進んでみてください。
□のある足し算
ではまず□のある足し算の解き方から、と行きたいところですが、まずは全ての四則演算に共通する考え方をご紹介していきます。それは計算の仕方を丸暗記するのではなく、小さい数だったらどうなるだろうと考えることです。例えば次のような問題があったとします。
□+2=5
この式の□に一体どんな数が当てはまるでしょうか。答えはもちろん3になりますね。こんな簡単な問題で何がわかるのかと思う方もいるかもしれませんが、それではどうして□が3という答えが求められたのでしょうか。それは5という和から2を引いたからに他なりません。このことから□が含まれる足し算は、和から□以外の数字を引くことで計算できるということがわかります。
このように複雑な計算の一部としてみるとわかりにくいことでも、小さい数を使うことで簡単に整理することができます。もし入試問題を解く上で□のある問題につまずいてしまったら、小さい数を使って一度計算の方法を確認してみるといいでしょう。
□のある引き算
では□のある引き算はどのように計算するのでしょうか。ここで重要なことが、□のある引き算には2つのパターンがあるということです。その2つとは、
- 左の引かれる数に□があるパターン(例えば□-2=5)
- 右の引く数に□があるパターン(例えば7-□=5)
というものです。そのため「引き算はこう計算する!」というやり方を暗記してしまうより、考え方の基本を覚えてしまう方がどんな問題と出会っても対応しやすいでしょう。その考え方の基本というのが、やはり小さい数で置き換えるというものです。ではまず①の引かれる数が□なパターンを考えてみましょう。いま、次のような例題があったとします。
□-2=5
この例題をもとに解き方をお教えしていきます。この問題の□に当てはまる数字はいくつでしょうか。ずばり答えは7になります。このような答えが出ることは読者の皆様もお分かりかと思いますが、ではどうして7という答えが出たのかを考えてくと、それは5と2を足したからでしょう。このことから、左の引かれる数に□がある引き算は残りの数を足すことで計算できるということが導けます。
それではこれと同じ手順で②のパターンについても、例題をもとに考えていきましょう。
7-□=5
この問題の□に当てはまる数は2になります。ではどうして2という答えが導けたのかを考えると、それは7から5を引いたからですね。このくらいのレベルの引き算だったら指を折りながら計算できますが、値が大きくなったらそうはいきません。そのため、このような小さい数の引き算の結果から分かる、右に□がある引き算は引かれる数から式の答えを引くことで計算できるということをしっかり頭に入れておきましょう。
□のあるかけ算
続いて□のあるかけ算の計算方法を考えていきましょう。□のあるかけ算の計算の解き方も、小さい数で試しに計算してみることでその根本の考え方は理解できます。かけ算は引き算と違い、かけられる数とかける数が逆でも答えは変わりません。そのため少し考えやすいのではないかと思われます。いま、
□×4=36
という式があったとしましょう。このとき□には9が当てはまりますよね。ではこの36とはどのような計算過程で導き出されたのかを考えてみましょう。おそらく36を4で割って求められたのではないでしょうか。このように□のあるかけ算は答えの数を□以外の数で割ってあげることで、かけ算の還元算・相当算を計算することができます。覚えておきましょう。
□のある割り算
それでは最後に、これまでと同じ手順で□のある割り算の計算について解説していきます。これも小さい数で考えることで計算の手順を見ていこうと思うのですが、ここで割り算には引き算と同じように2つのパターンが存在することを確認していきましょう。それは、
- 左の割られる数に□があるパターン(例えば□÷7=5
- 右の割る数に□があるパターン(例えば35÷□=5)
というものです。この2つの例題を見ても、答えは同じですが□に入る数字は全く違うことがよく理解できるのではないかと思います。それではまず順番に①のパターンから確認していきましょう。
□÷7=5
いまこのような例題があったとします。割られる数に□が来ていますが、この□には当然35という数が当てはまります。ではこの35がどのように求められたのか考えてみると、7と5をかけ算して計算した結果このような回答が導かれた、ということになるでしょう。つまり左に□が存在する割り算は、残った2つの数をかけ算すれば回答が導けるというわけですね。
他方②のパターンの問題はどのようにすれば解くことができるでしょうか、こちらも例題を取り上げながら少し考えてみましょう。
35÷□=5
こちらの問題では右側の割る数に□が来ていますが、この□にはもちろん7という数字が入ります。この7という答えはおそらく35を5で割った結果求められたものでしょう。したがって、割る数に□が存在する割り算に出会ったら、割られる数を答えで割ればいいということになりますね。
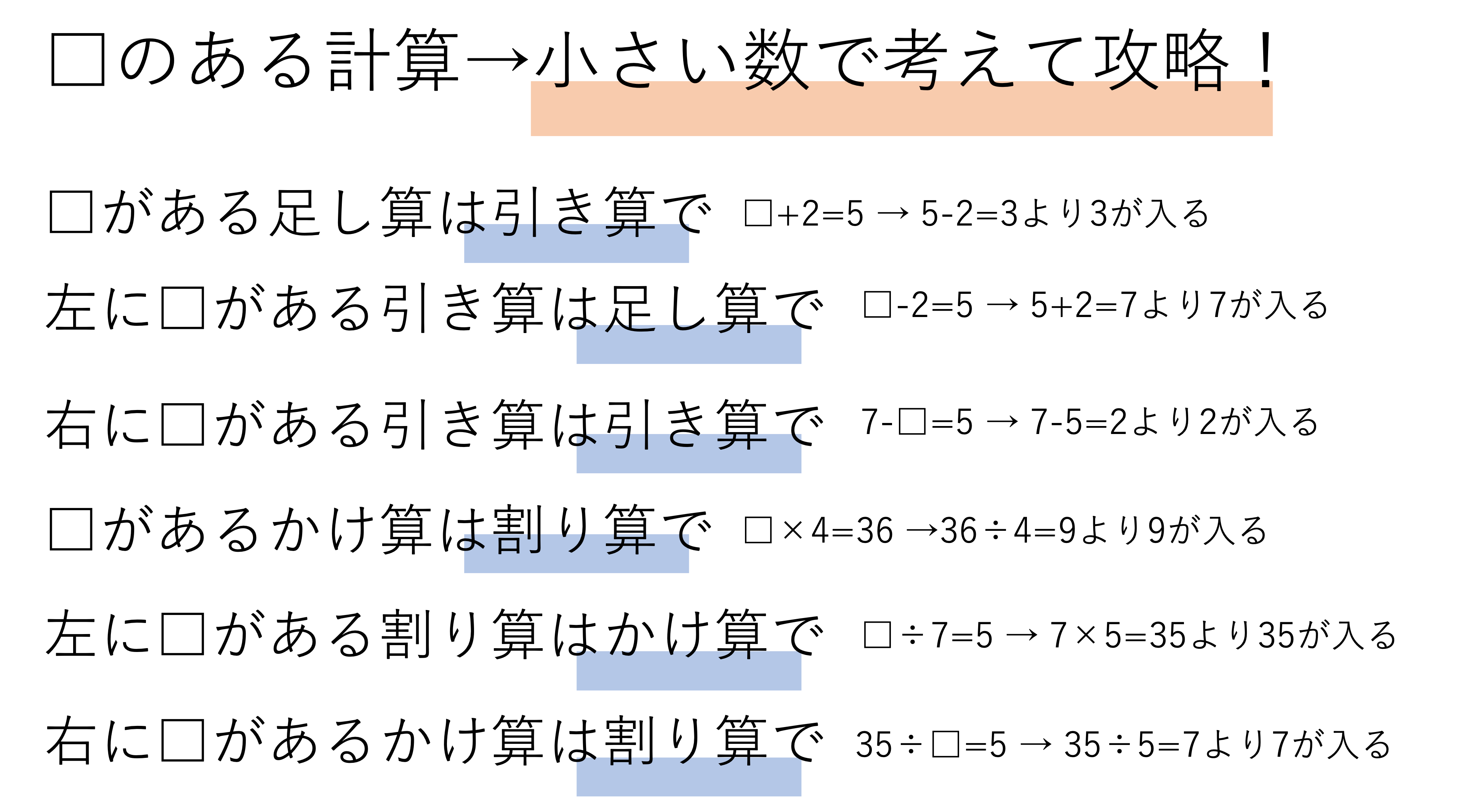
解き方まとめ!
これまで還元算・相当算の基本となる□のある四則演算の解き方をおさらいしていきました。大体の中身は小学校で習った確かめ算と同じですが、それでも文章題や複雑な問題を意識して取り組むのには大きな意義があるのではないでしょうか。今回□のある計算を振り返るにあたって活用した、小さい数で式を簡単にしてみてから考えるという方法も色々なところで使えるものです。ぜひ覚えておきましょう。
複雑な問題のときは…?
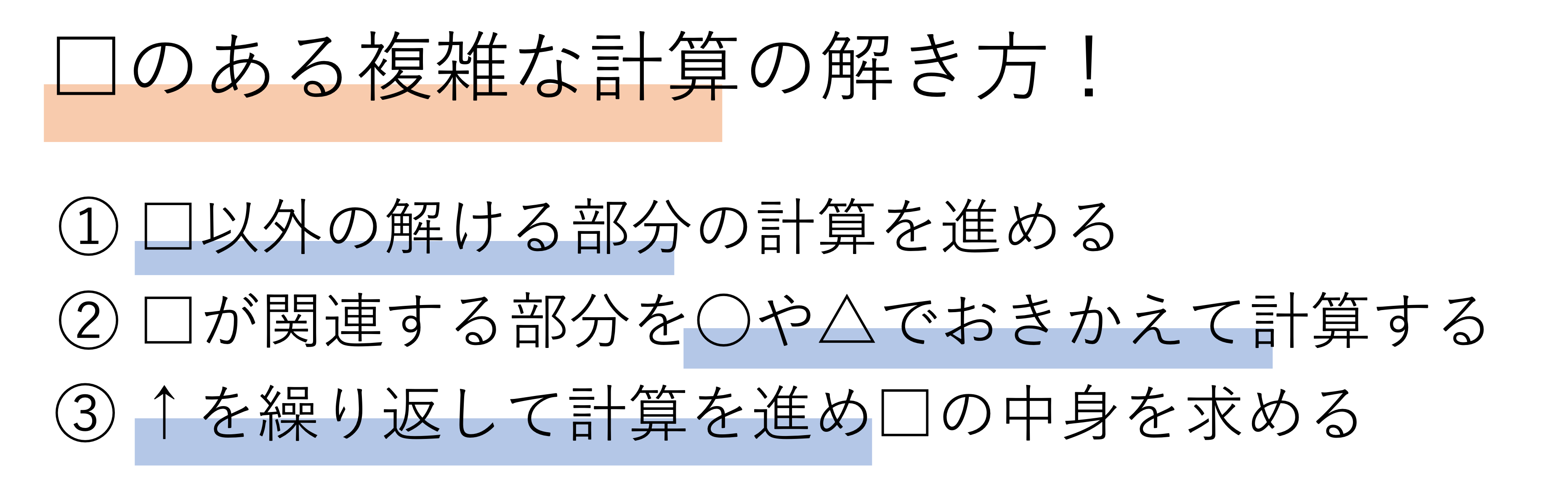
以上で取り上げたのは単純な+・―・×・÷の計算、いわゆる基礎的な四則演算に過ぎません。中学受験ではこれ以上に複雑で難しい算数の問題が山ほど登場することは、この記事を読んでいる親御さんもお子様もよく理解していることでしょう。先ほどあげた例題でも、いくつもの符号やかっこが登場していましたが、このように還元算・相当算というのは一筋縄ではいかないものばかりです。ではこのような複雑な問題はどのようにして解けばいいのでしょうか。一つ例を使いながらご紹介していきましょう。
38÷(89-70)×(□+8)=104
まずこのような問題で大切なことは、一度□を考えずに出来る範囲の計算を正確にこなしていくということです。今回の問題であれば、38÷(89-70)の部分が□の中身に関係なく計算できそうです。このような計算を行う理由は、式を簡単にできるからです。中身を見て仕舞えば簡単な問題でも、数字と符号がたくさんあるというだけで難しく見えてしまうものです。
さっそく式を整理してみましょう。38÷(89-70)を簡単にするには、まずかっこの中の引き算を行う必要がありますね。その結果38÷19という式ができるのですが、この割り算をさらに解いてみると答えは2となります。そうして求まった計算結果を改めて式の中に当てはめてみましょう。
38÷(89-70)×(□+8)=104
2×(□+8)=104
ここからが少し工夫のいるポイントになります。実はここまで計算しても、まだ□を直接求めることはできません。算数の得意な人だったら暗算できてしまうかもしれませんが、一度工夫の仕方を抑えておきましょう。ここで行う対処とは、□+8という部分を別の文字で置き換えて計算してみるということです。置き換えるとは、次のような操作を指します。
2×○=104
このようにすると、単純な四則演算の形が出来上がり、◯の中身が52だということが瞬時に計算できるかと思います。そして丸の中身がわかったら、今度は次のような式も出来上がりますね。
○=□+8=52
そして足し算の還元算・相当算の解き方に従うと、□の中身が44だと計算できます。このように、□などのまだわからない部分・最終的に求めたい部分が含まれる箇所を別の文字において、段階を分けて計算を進めていくというテクニックは、早く正確な計算を行う上で重要です。急がば回れという諺もありますが、ぜひこのようなワンテンポ置く技術を身につけてみて下さい。
まとめ
今回は還元算・相当算の解き方についてご紹介していきました。還元算・相当算という単語に聞き覚えは無かったかもしれませんが、この□を使った計算というのは中学受験において欠かせないものです。そのためこの記事以外にも、おすすめ記事や参考文献を活用しながら、更なる学力向上を目指しましょう。本記事が今後の学習のお役に立てば幸いです。


















