この記事では「消去算」の解き方を解説していきます。問題を一緒に考えながら、基本の解き方を学んでいきましょう。
Contents
消去算とは
消去算とはいくつかの分からない数を、式を操作することで、その数を求める問題です。
これでは分かりにくいと思うので例題を出してみます。
-
りんごを3個、みかんを5個買うと490円になります。また、りんごを4個、みかんを3個買うと470円になります。りんごとみかんはそれぞれ何円でしょう。
-
りんごを6個、みかんを5個買うと720円になりました。りんごはみかんよりも10円高いとすると、りんごとみかんはそれぞれ1個何円でしょう。
-
りんごを4個、みかんを1個、レモンを2個買うと560円になりました。りんごを1個、みかんを4個、レモンを3個買うと440円になりました。りんご3個とレモン1個を買うと何円になるでしょう。
なんとなくどんな問題かイメージできましたか？これが消去算の基本形です。それではさっそく問題を解いてみましょう。
消去算の解き方
基本的な問題（問題☆、問題①）
先ほど例であげた問題①を解く前に、次の問題を考えてみましょう。
（問題☆）レモンを3個、アボカドを4個買うと640円になります。レモンを3個、アボカドを3個買うと540円になります。レモンとアボカドはそれぞれ何円でしょう。
これを図にまとめると以下のようになります。
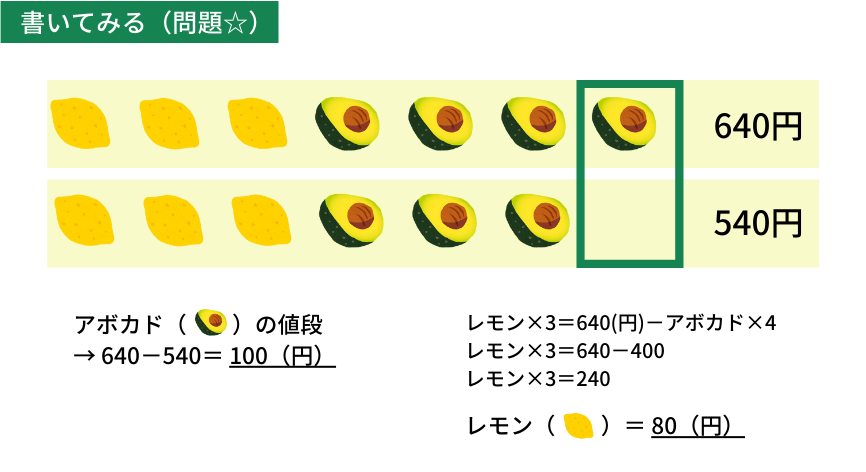
上と下を比べることで、アボカド1個の値段は\(640-540＝100\)円だとすぐ分かりますね。
アボカドの値段が分かれば、後はレモンとアボカドの合計金額からアボカドの値段を引いて、レモンの個数で割ればレモンの値段は分かります。（図を見るとわかりやすいです）
これを解くと、レモンは\(（640-100\times4）\div3＝80\)（円）となります。
問題☆がわかった上で、問題①を考えていきましょう。
（問題①）りんごを3個、みかんを5個買うと490円になります。また、りんごを4個、みかんを3個買うと470円になります。りんごとみかんはそれぞれ何円でしょう。
まずは図でまとめてみます。
問題☆はレモンの数が同じだったため、単純に2つの金額の差をとることでアボカドの値段が求められました。
しかし、今回は図の上と下でりんごの数とみかんの数が両方異なるため、問題☆のように単純に差を取って求めることはできません。では、どうすれば求められるでしょうか？
「どちらかの個数が揃っていれば求められる」ということは「どちらかの個数を揃える」ということをすれば、両方個数が異なっていても求められるということです。
実際に問題①を解いて見てみましょう。「どちらかの個数を揃える」ためには、何をすれば良いでしょうか？
正解は、上と下（2つの組み合わせ）をそれぞれ何倍かして、どちらかの個数を合わせる、です。最小公倍数の考え方ですね。
今回はりんごの方が少ないので、りんごの個数を合わせていきます。
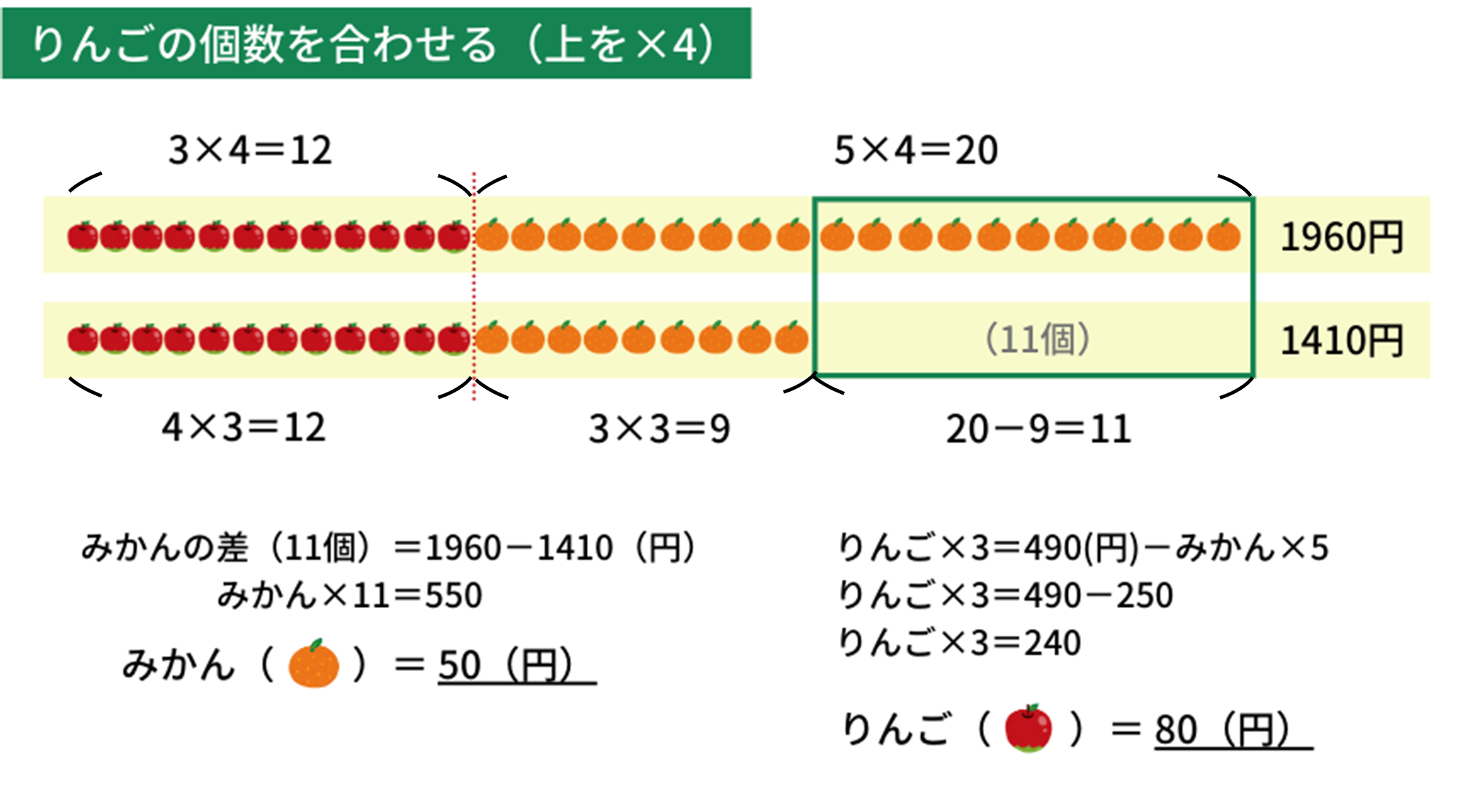
りんごは\(3\)個と\(4\)個なので、\(3\)と\(4\)の最小公倍数である\(12\)個にします。\(3\)個の方（上）には\(\times4\)、\(4\)個の方（下）には\(\times3\)します。合計金額も忘れずに変えましょう。
すると、りんごの数は両方とも\(12\)個、みかんの個数は上の方が\(5\times4＝20\)（個）で、下の方が\(3\times3＝9\)（個）になります。
みかんの個数の差は\(11\)個で、金額の差は\(1960-1410＝550\)（円）です。ということは、みかん\(\times11＝550\)（円）なので、みかん1個の値段は\(550\div11＝50\)（円）と求まります。
みかんの値段がわかったら問題文のままの式に当てはめましょう。（かけ算した後の式でももちろん大丈夫ですが、数が大きくなってしまうので前の方がおすすめです）
ここでは、りんご\(\times3+\)みかん\(\times5＝490\)（円）の式に当てはめて、りんご1個の値段は\(（490-50\times5）\div3=80\)（円）だとわかります。
この問題はみかんの個数を合わせることでも解けるので、是非自分でやってみましょう。個数を合わせるときは\(3\)と\(5\)の最小公倍数で合わせます。
少し変わった問題（問題②）
次に、少し変わった消去算の問題を解いてみましょう。
（問題②）りんごを6個、みかんを5個買うと720円になりました。りんごはみかんよりも10円高いとすると、りんごとみかんはそれぞれ1個何円でしょう。
まずは図にまとめてみましょう。
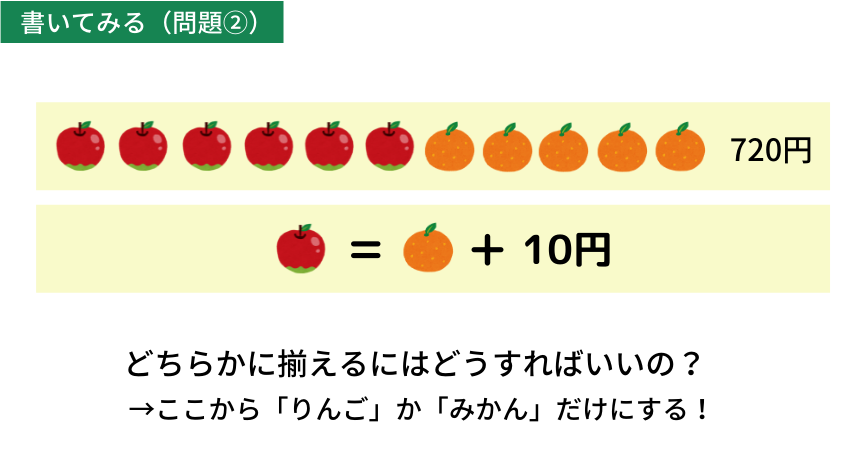
ここまで見てきたように、消去算で大切なことは、2種類のもののうち片方の数を揃えて、もう片方だけにすることです。
先ほどの問題では最小公倍数で揃えましたが、今回の問題ではどうすれば良いでしょうか？
この問題では2つ目の式が特徴的ですね。りんごはみかんで、みかんはりんごで表せるので、置き換えるのが良さそうです。
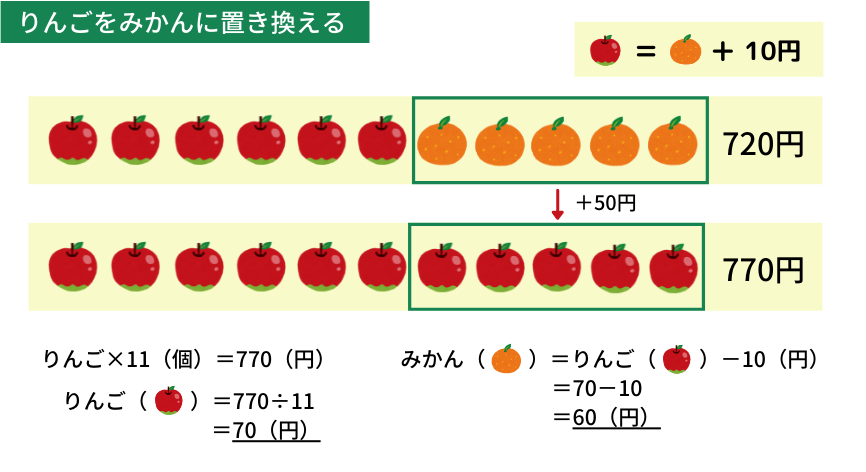
みかん\(1\)個をりんごに置き換えると、合計金額は\(10\)円増えます（みかん\(＝\)りんご\(-10\)円）。なので、みかんを\(5\)個ともりんごに置き換えると、合計金額は\(720＋10\times5＝770\)（円）になります。
よって、りんご\(\times11＝770\)（円）なので、りんご\(1\)個は\(770\div11＝70\)（円）だと求まります。みかん＝りんご\(-10\)円なので、みかん\(1\)個は\(70-10＝60\)（円）です。
今回はみかんをりんごに置き換えましたが、りんごをみかんに置き換えても解けるので是非やってみましょう。
消去算の解き方 まとめ
ここまで見てきた消去算の解き方をまとめておきます。簡単な問題でも、難しい問題でも、この３ステップが大切です。
- 図を書いて状況を把握する
→書くときは自分がわかればＯＫ！ - 2種類のもののうち片方を消去して片方だけにする
→最小公倍数で揃えたり、どちらかで置き換えたりしましたね！ - 個々の値を計算する
→問題文をもう一度見て、何を問われているのか確認しましょう！
消去算の応用
最後に、応用問題をご紹介します。気になる方はぜひ解いてみてください。
（応用問題）りんごを4個、みかんを1個、レモンを買うと560円になりました。りんごを1個、みかんを4個、レモンを3個買うと440円になりました。りんご3個とレモン1個を買うと何円になるでしょうか。
応用でも解き方はこれまでと同じです。1つずつ確認していきましょう。
①図を書いて状況を把握する
とりあえず図を書いてみましょう。
②2種類のもののうち片方を消去して片方だけにする
今回は3種類ですが、やることは2種類の時と大して変わりません。聞かれているのはりんごとレモンなので、みかんを消去することでりんごとレモンだけにしましょう。
みかんは上が\(1\)個、下が\(4\)個なので、問題①のように最小公倍数で合わせれば良さそうです。上の方を\(4\)倍しましょう。
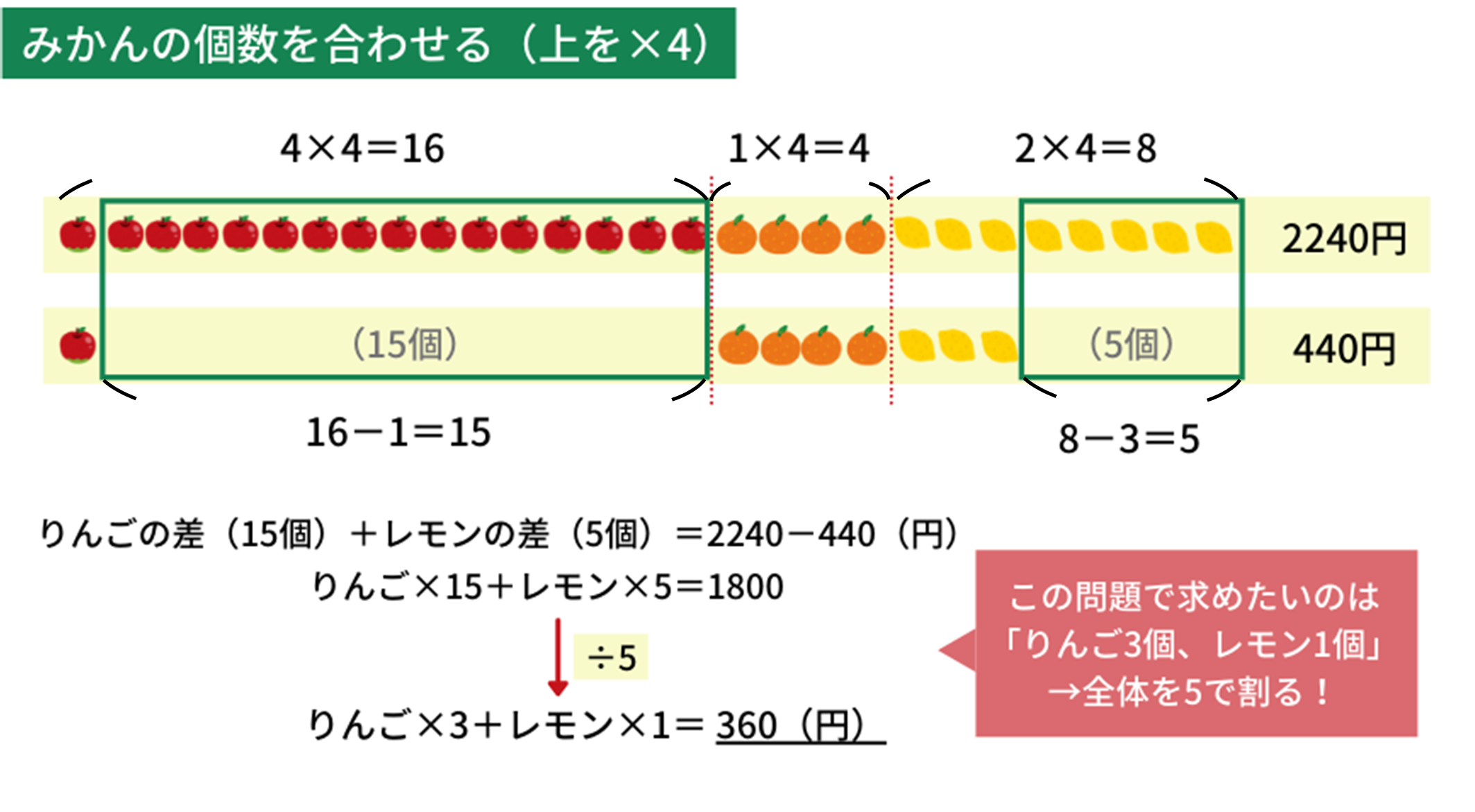
すると、上の方は「りんご\(16\)個、みかん\(4\)個、レモン\(8\)個」になるので、下との差はりんごが\(15\)個、レモンが\(5\)個だとわかります。
金額の差は\(2240-440＝1800\)（円）なので、りんご\(\times15＋\)レモン\(\times5＝1800\)（円）です。みかんを消すことができましたね。
③個々の値を計算する
この問題では\(1\)つずつの値段ではなく、「りんご\(3\)個とレモン\(1\)個の値段」を求めたいのでした。これは先ほどの「りんご\(\times15＋\)レモン\(\times5＝1800\)（円）」の式の全体を\(5\)で割れば求められます。計算すると、\(1800\div5＝360\)（円）です。
問われているのが1つずつの値段ではないとき、問われている式が出るかもと考えるのも良いかもしれません。（今回の場合は「りんご\(\times3＋\)レモン\(\times1＝\)？」が出るのかな？と考えます）
別解
全体の個数を見た面白い別解もあります。
上下を足すと、りんご、みかん、レモンのすべての個数が\(5\)個になります。つまり、りんご\(5\)個、みかん\(5\)個、レモン\(5\)個の値段が\(560＋440＝1000\)（円）だと求まります。（りんご\(\times5＋\)みかん\(\times5＋\)レモン\(\times5＝1000\)）
これを\(5\)で割ることで（りんご\(1\)個\(＋\)みかん\(1\)個\(＋\)レモン\(1\)個）の値段は\(200\)円だと求まります。
あとは、上の方の式（りんご\(\times4＋\)みかん\(\times1＋\)レモン\(\times2＝560\)）を使って求めます。つまり、（りんご\(1\)個\(＋\)みかん\(1\)個\(＋\)レモン\(1\)個）を引いてあげれば、りんご\(3\)個とレモン\(1\)個の値段がわかるというわけです。これを解くと、\(560-200＝360\)（円）です。
練習用プリント（無料）
練習用プリント（無料）は、
『個別指導塾テスティー』の公式LINE の友だち追加された方のみの配布となっております。
以下から公式LINEの友だち追加をして、記事の続きをお楽しみください！！
＜スマートフォンからお読みの方はこちら＞
＜パソコンからお読みの方はこちら＞
まとめ
消去算で大切なのは、ものの種類を減らしたいという考え方です。
慣れてきたら「これに揃えれば計算が少なくてすむな」「この問題工夫して解けそう！」などと考えられるといいですが、まずは面倒くさい解き方でも答えを出してみましょう。
解答と違ったら解き方を真似してみればいいですし、同じだったら違う解き方でも解いてみると勉強になります。
消去算は色々な問題に使える考え方なので、ぜひマスターしましょう。この記事が少しでも参考になったら嬉しいです。
おすすめ記事
参考
東京大学理科二類の岡部信です。
京都の高校に通っていたので東京は知らないことだらけです。特に通勤電車はすし詰め状態だと聞いていましたが、ここまでだとは思ってなかったです。実家では犬を飼っていたのですが、もう3ヶ月近く会っていないのでそれが1番寂しいです。今は千葉で父と姉と3人暮らしですが、9月からは東京で1人暮らしする予定なので楽しみです。大学ではテニスサークルと東大村塾という農業と村おこしを掛け合わせたような活動をしているサークルに入っています。趣味は料理、登山です。料理は高校の時に料理研究部に入っていたのでそこそこ出来ますが、もっと上手くなれるよう時間がある時は夕ご飯を作ったりしてます。お菓子も色々作れるようになりたいです。登山は友達と休日に日帰りで行ったり、夏休みは泊まりで行ったりもしてます。今年の夏は富士山と北海道の富良野岳に行く予定です。
皆さんよろしくお願いします。
