この記事では力の種類について述べる.前回までに見てきたニュートンの3 法則でも「力」というものが登場したが,これらの原理はその力がどうして発生しているかについては何も語らない.運動方程式の意味をもう一度思い出そう.運動方程式
\(m\overrightarrow{a} = \overrightarrow{F}\) (1)の意味は,右辺の力が「原因」となって左辺の加速度が「結果」として生じるのであった.逆に言うと,物体の質量と加速度が求まったからといって,「力が求まった」ということにはならないのである.
では力はどのように計算するのかというと,実験や経験から「こうなる」ということを受け入れるのである.つまり今までの人たちが発見した「公式」を覚えるのである.もちろん,物理の研究としては「なぜそのような力が生じるのか」という疑問も探求するのだが,大学受験においては公式を覚えるだけで十分である.そもそも力についての研究は未だにされているし,高校範囲で到底理解できるとは思えない.ここでは受験に必要な力の最低限度の知識を挙げることにするが,つまづきそうな部分は丁寧に述べたつもりである.そのため記事は2 つに分割したので両方とも確認してほしい.また,電磁気学で登場する力についても軽くまとめておく.詳しくは電磁気学の記事で学んでほしい.電磁気学をまだ習っていない人は,飛ばして構わない.この記事は最終的には覚えるべき力の公式集となるようなつもりで書いてある.最後に発展的な内容も書いたので,興味のある人は読んでみよう.
Contents
公式のある力と公式のない力
まず力の種類を覚える前に,力を大きく2 つに分類しておく.この分類は力の本質の分類というよりも,実際に受験問題で力を計算するにあたっての分類である.公式のある力はその公式を覚えること.そして公式のない力はどのように求めるのか.この2 つのことを意識して読み進めてほしい.
公式のない力
先に公式のない力について述べよう.結果からいうと公式のない力は後の記事で紹介する「束縛条件」というものから計算する.だからここでは詳細な計算は述べずに,どのような力が公式のない力なのかということを知っておくだけで十分である.
垂直抗力
物体を床に置いた時,床が物体を支えるように床に垂直に力が働く.これを垂直抗力という.物体が別の何かと接触している場合,そこには必ず垂直抗力が働く.頬杖がつけるのも垂直抗力のおかげである.
張力
ひもや糸が物体と接続しているときに,物体がひもや糸から受ける力を張力という.問題で出題される場合はひもや糸はぴんと張った状態(たるみのない状態) の張力を問うことがほとんどである.
静止摩擦力
後に述べるように摩擦力には3 つあるが,その内静止摩擦力だけは公式がない力である.静止摩擦力は物体が滑らないように働く力である.
公式のある力
ここで述べるのは公式のある力なのでしっかりそれを覚えてほしい.自分で公式を紙1枚くらいにまとめておいて,問題を解く際の参考にするのも良いだろう.
重力
質量\(m\)の物体には重力が働き,
\(F = mg\) (2)である.ここで\(g\)とは重力加速度であり,
\(g = 9.8 m/s^{2}\) (3)である.
重力加速度とは地表付近の物体が自由落下1するときの加速度である.これは地球での値で,例えば月だと異なった重力加速度になる.多くの問題で「重力」と言われれば,地表付近の重力を考えているので上の公式を覚えればよい.
万有引力
以下の図のように質量\(m\)の物体と質量\(M\)の物体があったとき,それらの物体間には万有引力が働き,
\(F = G\frac{mM}{r^{2}}\) (4)である.ここで\(G\)は万有引力定数で,
\(G = 6.67\times 10^{-11}Nm^{2}/kg^{2}\) (5)という値を持つ.
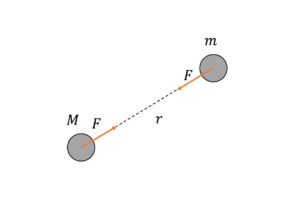
図1:質量mの物体と質量M の物体の間には万有引力F が働く.
この力は質量を持つあらゆる物体に働く引力なので「万有」引力と言われる.この力は自分と身の周りにいる人の間にも働いているが,その力を感じることはないだろう.それは万有引力定数の大きさに原因がある.
\(10^{-11}\)という値がかかっていることからも分かるように,万有引力が実生活で感じられるようになるためには,質量が大きいものでないといけない.万有引力が感じられるのは例えば天体による万有引力である.だから地球上にいる場合は,地球と自分との間の万有引力しか感じられないのである.
さて,重力と万有引力というものを紹介したが,何が異なるのだろうか.(あまり言葉に慣れていない人は,ひとまずそれぞれの公式を覚えて,この部分を飛ばしても構わない.) 結果から言うと,本質的にはどちらも同じものである.ここで言葉を分けた理由は入試問題の使われ方に沿うようにしたからである.つまり問題で「重力」と言われた場合の多くが\(F = mg\)の公式であり,「万有引力」と言われた場合が\(F = G\frac{mM}{r^{2}}\)を用いるのである.
では同じものなのになぜ公式が異なるのか.「重力」のところでも敢えて下線を引いたが,\(F = mg\)の公式は地表付近の力を表すと書いた.どういうことかを式で見ていこう.地球の質量と半径をそれぞれ\(M\),\(R\)とすると,地球上の質量\(m\)の物体に働く万有引力は,
\(F = G\frac{M}{R^{2}}m\) (6)となる.この\(m\)の係数は(地球の質量や大きさが変わらない限り) 定数であるからそれを\(g\)と置いてしまう.するとこれはまさしく重力の公式になる.つまり重力加速度とは
\(g = \frac{GM}{R^{2}}\) (7)
のことである.上の式に実際の地球の質量と半径を調べて計算してみよう.だいたい\(9.8 m/s^{2}\)になるはずである.
弾性力
弾性力とは物体を変形したときに元の形に戻ろうとする力2である.入試問題では主にばねが登場するので,ここではばねの話をする.
以下の図のように一方の端を壁に固定し,もう一方の物体が付いている部分を押したり,引いたりすることを考える.経験的にばねを引き伸ばすと縮む方向に力が働き,ばねをぐっと押し縮めると伸びる方向に力が働くことを知っているだろう.また伸ばせば伸ばすほど,あるいは縮めれば縮めるほど,その力が大きくなることも分かる.
ばねに全く力を加えていないときのばねの長さを自然長という.ばねの伸びが\(\left| x\right|\)のとき,物体はばねから
\(F = k\left| x\right|\) (8)の大きさの力を受ける.(\(x\)の値は負になり得ることに注意.) ここでk はばね定数でばねの伸びにくさを表している.\(k\)の値が大きいほど,伸ばすのに大きな力を要することが分かる.そしてこのばね定数はばねが何でできているかなど,ばねの性質で決まるものなので,問題では予め値が与えられていることも多い.
さて絶対値がつくとそれだけで複雑に思う人もいつかもしれないが,しっかり場合分けをして考えよう.まずばねが伸びているとき,すなわち\(x > 0\)の時,\(\left| x\right| = x\) である.このとき左向きに力が働くから向きも考慮すると,
\(F = -k\left( +x\right) = -kx\) (9)となる.逆にばねが縮んでいるとき\(x < 0\)ゆえ,\(\left| x\right| = -x\)である.このとき右向きに力が働くから向きも考慮して,
\(F = +k\left( -x\right) = -kx\) (10)となる.つまりばねが伸びていようが縮んでいようが,その弾性力は同じ形で表される.今見たように,物体が伸びている図でも,縮んでいる図でも向きなどに注意すれば同じ式になるのだが,この符号を間違えることが多い.そこでばねの力を考えるときは,「ばねののびが正の位置にある状態の図を描いて考える」のが分かりやすい.
そうすれば,弾性力の向きだけで符号が判断できる.ここまでの説明だけであまりピンとこなかった人は,物体が伸びている状態と縮んでいる状態,座標の向きが右向きの場合と左向きの場合の組み合わせの4 通りの図を描いて,その符号がどうなるか確かめてほしい.
ここからは余談だが,この公式は実際は「近似的に」正しいものである.例えばばねをずっと伸ばしていくとあるところで急に伸びやすくなったり,最終的には破断してしまったりする.しかしある程度の伸びまでであれば,力の大きさは伸びに比例することが分かっている.問題では暗黙の内にこのように伸びに比例すると見なしても問題ない範囲での物体の動きを対象としている.だからいなるときも弾性力が上の公式のようになるという訳ではない.
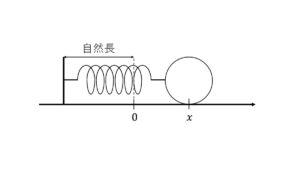
図2:ばねに接続された物体が,ばねが伸びた位置にある場合の図.
空気抵抗力
空気抵抗を受ける物体の問題は問題文中に力がどのように書かれるかが示されていることも多いが,念のため紹介しておく.ある物体が速さ\(v\)で運動しながた空気抵抗を受けるとき,その抵抗力の大きさは
\(F = \gamma v\) (11)で表される.ここでこの力の向きは速度とは逆(運動方向とは反対の向き) に働く. \(\gamma\)3はその比例定数である.弾性力の余談でも述べたのと同様に,これもいかなる空気抵抗が上の公式になるという意味ではない.ただ,入試で問われるのは基本的に速さに比例する場合であるから,この公式を覚えておけばよい.
1自由落下とは重力以外が働かない物体の落下である.本来物理では「自由」と言ったときは「力が全く働かない」ことを意味するが,自由落下だけは「自由」というのが慣習である.
2「復元力」と書かれている場合もある.
3「ガンマ」と読む.
おすすめ記事
参考
こんにちは。慶應義塾大学大学院物理学科の花井遼介です。
中学から大学生の前半くらいまではバドミントンをずっとやっていましたが、途中から勉強や研究が忙しくなり、最近ほとんどやっていません。なかなか運動をする機会が減って残念ですが、時々自転車の乗って知らない場所に行ったり、散歩をしたりしています。(特に研究に行き詰ったとき……)昔から理科が好きで、高校生の時に聞いた、とある物理学者の講演に感動して以来、大学では物理を専門に学びたいと思っていました。現在は原子核理論の研究室に所属しています。その中でも僕は中性子星という超高密度な天体を、原子核理論の立場から研究しています。物理が好きでそれを専ら学んでいることもあって、高校生向けに高校物理や大学に入ってからの物理、物理学科についてなどの記事を提供していこうと思います。高校物理の記事でも、僕が大学に入って得た知識や理解をもとに、受験に役立つのみならず、学問としての面白さが含まれるような記事を書くつもりです。(受験向けの部分とそうでない部分は分かるように書くつもりですので、興味や必要に応じて読んでもらえればと思いま。)
僕の書く記事は、あくまで読者の皆さんの「補助的なもの」です。最終的には自分で勉強する、ということが大事になります。なので記事をきっかけに、皆さんが自分で物理を勉強できる状態になれれば、僕の目標は達成されたことになります。
僕の記事からさらに自分でもさらに深く勉強してほしいと思います。
皆さんと共に物理の面白さに触れ、理解を深められることを願っています。





















