Contents
溶解するとは…?
NaClが水に溶ける時には実は水和という現象が起きている。
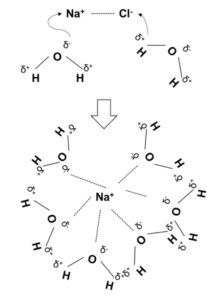
図1
まず、極性分子であるH2OはHがδ+、Oがδ–の極性を示している。
Hのδ+がCl–へ、Oのδ–がNa+へと近づき、電気的な引力を互いにはたらかせることで、NaClをNa+とCl–に電離させる。
その後、図1のようにNa+およびCl–を大量に存在するH2O分子が取り囲む。
この現象を水和といい、これが溶解している状態である。この原理からも分かるように、溶媒は水でなくとも他の極性溶媒であったとしても溶ける。
つまり、極性分子は極性溶媒に溶けやすい。
一方、I2(ヨウ素)などの無極性分子は極性溶媒には溶けにくいが、同じ仲間の無極性溶媒(C6H6ベンゼンなど)とは混ざりやすい。
これは溶質分子の分子間力と溶媒分子の分子間力が同程度に弱いからである。
※図1はCl–も同様
固体の溶解度
固体の溶解度とは
溶媒100gに溶かすことのできる溶質の質量(g)を固体の溶解度といい、限界まで溶け切った溶液を飽和溶液という。
★発展
実際には飽和状態でも溶解はすすんでいる。溶け切るということではなく、固体から溶け出す粒子数と溶液から析出する粒子数が落ち着き、等しくなったため、見た目上溶け切って変化しないだけである。
気液平衡の時と同じく、これは溶解平衡と呼ばれている。
※固体の中にはCuSO4・5H2Oのように水和した水分子を含むものもあり、水和物と呼ばれる。
加熱するとH2Oをとばして無水物CuSO4にすることができる。
一般に固体の溶解度は温度が高くなればなるほど大きくなることが多い。
これを利用して、高温で溶けるだけ溶質を溶かして飽和溶液にした後に、一気に低温にすることで溶け切れなくなった溶質を析出させることができる。
このような精製方法を再結晶といい、少量含まれている不純物は析出しない点が、単に溶媒を蒸発させる時より優れている。(不純物が飽和に達しない)
例題
- KNO3は水100gに、80℃で169g、25℃で38g溶ける。いま80℃のKNO3の飽和溶液400gを25℃に冷却すると何gのKNO3が析出するか?
- CuSO4の無水物の溶解度は、水100gに60℃で40g、10℃で15gである。60℃のCuSO4の飽和水溶液200gを10℃に冷却したら、CuSO4・5H2Oは何g析出するか?
【解答】
- 気をつけたいのは水400gにKNO3を溶かすわけではなく、溶かしてある飽和溶液が400gという点である。
もし水が100gなら80℃→25℃で169 – 38 = 131g析出する。
いま、水の量は100g ×\(\frac{400}{269}\)gなので、
析出量は 131 × \(\frac{400}{269}\)≒ 190g - 水和物の析出の問題は一筋縄ではいかず、析出量を文字で置くなどの工夫が必要である。
まず、60℃のCuSO4の飽和水溶液200g中にCuSO4は、40g ×\(\frac{400}{140}\)≒ 57g 含まれる。ここからCuSO4・5H2Oが析出するとCuSO4だけでなく水の量も変わるので、ひとまずCuSO4・5H2Oをx gとおいで式を立ててみる。
CuSO4・5H2O(式量:250)より、CuSO4(式量:160)は、 x × \(\frac{160}{250}\)g 析出
H2O (式量:90)は、 x × \(\frac{90}{250}\)g 析出する。
いま、10℃では115gの飽和溶液中にCuSO4は15gまで溶けるので、同じく、200 – xのCuSO4aq中にCuSO4は 57 – x × \(\frac{160}{250}\) g溶けるので、
115 : 15 = (200 – x)(57 – x × \(\frac{160}{250}\)) を解いて
x ≒ 61g
気体の溶解度
気体の溶解度とは
気体の溶解度は標準状態で溶媒1Lに何Lの気体が溶けるのかで表すことが多い。
一般に気体の溶解度は温度が高くなると小さくなっていく。
これは気体分子の熱運動が激しくなって溶液から飛び出しやすくなるからである。(固体の溶解時には温度が高い方が結合エネルギーを切りやすくなる得の方が大きかった。)
気体の溶解に関する重要な法則をここで1つ紹介する。
〈ヘンリーの法則〉
水にとけにくい気体に関して、
一定温度の下では水にとける気体のmol数(質量)は気体の圧力に比例する。
(→簡単のため水にしたが一般の溶媒で成り立つ。)
これは温度が一定なら、気体の圧力を2倍、3倍…とかけると、溶ける気体のmol数も2倍、3倍…と比例するということである。
ただし、これが成立するのはもともとその溶媒への溶解度が大きくない気体のみであることに注意。また、溶ける気体の体積も2倍、3倍…となりそうだが、ボイルの法則より圧力が2倍、3倍…となると体積は1/2倍、1/3倍…となることから相殺されて体積は一定。
例題
- 0℃、01×105paの空気が水1.0Lに接しているとき、溶解するO2の質量(g)とその分圧下での体積(mL)はいくつか?ただし空気はO2とN2が1:4で混合しており、0℃、1.01×104paのO2は水100mLに7.0×10-4g溶けるものとする。
- 内容積の調節可能な容器に1.0molの気体Aと10Lの水を入れた。Aの水への溶解にはヘンリーの法則が成立し、温度32℃、圧力1.0×105paのとき水1Lにつき0.050Lとける。また、32℃、1.0×105paのA1.0molの体積は25Lとする。
⑴容器内の圧力が1.0×106paのとき、Aの溶解後の気体部分の体積は何Lか?
⑵Aの溶解後の気体部分の体積から4.5Lのとき容器内の圧力は何paか?
⑶0.40molのAが水に溶けた時、容器内の圧力は何paか?また、Aの溶解後の気体部分の体積は何Lか?
【解答】
- まず同温同体積ではドルトンの分圧の法則より分圧比=mol比となるため、接している空気のうち、O2の分圧は1.01×105×\(\frac{1}{5}\)paである。いま、
0℃、1.01×104 pa、 水100mL に O2は7.0×10-4gとける。
問いは 0℃、1.01×105×\(\frac{160}{250}\)pa、 水1L に O2は □gとける
なので、ヘンリーの法則より7.0×10-4×10×2=1.4×10-2g
また体積はヘンリーの法則関係なく一定なので、水の量の10倍だけ計算し、
7.0×10-4×10=7.0×10-3gが何mLかを求めればよい。7.0×10-3 / 32 molなので
22.4×7.0×10-3 / 32 = 4.9×10-3L ∴ 49mL
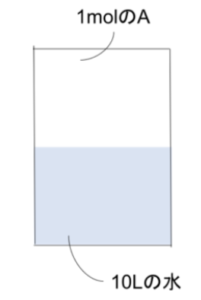
図2
⑴気体Aは32℃、1.0×105pa、水1L につき0.050Lとけるので、
32℃、1.0×105pa、水10Lにつき 0.50Lとける。
Aが溶ける体積は圧力によらず一定なので、容器内が1.0×106paでもとけるAは0.50Lである。
ところで溶解前のAは1.0×105paでは25Lなのでボイルの法則より
1.0×106paでは2.5L存在した。よって、溶解後は2.5 – 0.5 = 2L
⑵⑴と同様にして、圧力によらず溶けるAの体積は0.50Lなので、溶解前のAの体積は5.0Lであったと求まる。圧力が1.0×105paのときAは25Lなのでボイルの法則は、圧力は5.0×105pa
⑶圧力1.0×105paのとき、10Lの水に0.5L=0.02molとける。(∴ 1mol=25L)
ヘンリーの法則によると、圧力と溶けるmol数は比例するので、0.4mol溶けたとすると圧力は2.0×106pa
圧力が2.0×106paのとき、溶解前のAの体積はボイルの法則より1.25Lと求まるので、溶解後は1.25 – 0.5 = 0.75L
質量モル濃度
これまでに質量パーセント濃度とモル濃度という2つの濃度表示を見たが、ここで1つの新しい計算方法を導入する。
質量パーセント濃度 → 溶質の質量(g) / 溶液の質量(g) × 100
モル濃度 → 溶質のmol / 溶液の体積(L)
new! 質量モル濃度 → 溶質のmol / 溶媒の質量 (kg)
質量モル濃度の分母は溶媒の質量であるというのが大きな特徴である。
質量を用いると温度変化によって体積が変わる場合でも使えるので、この8章のように溶液の温度を変えていく際によく用いられる。
蒸気圧降下
蒸気圧降下とは
純粋な水と、水に少量の砂糖を溶かした砂糖水を比較した時に蒸気圧はどう異なるのかを考えてみる。
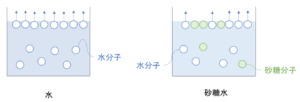
図3
蒸気圧というのはどのくらい溶媒分子が蒸発しようとするのかという力のことであった。
いま、上の図を見ると分かる通り、液体の表面から蒸発しようとする水分子の数が、砂糖水は砂糖分子のせいで減ってしまっている。
つまり、蒸気圧は下がってしまっている。
このように、ある溶媒に不揮発性の溶質が溶けた溶液の蒸気圧は何も溶けていない純溶媒の蒸気圧に比べて低くなる。これを蒸気圧降下という。
蒸気圧が下がる度合いは何が溶けているかという溶質の種類は関係なく、どのくらい溶けているかという溶質の質量モル濃度に依存する。
ラウールの法則
★発展
〈ラウールの法則〉
前のページの図を見て予想できるように、砂糖水の蒸気圧は本来の純水の蒸気圧に、水分子のモル割合であるモル分率をかけたものとなる。
すなわち、純水の蒸気圧 : P0
砂糖水の蒸気圧 : P
水分子のmol : n0
砂糖分子のmol : n1 とすると、
これを変形していくと、
\(P=P_{0}\times\frac{n_{0}}{n_{0}+n_{1}}\)\(=P_{0}\times(1-\frac{n_{0}}{n_{0}+n_{1}})\)
→ \(= P_{0}-P = \frac{n_{1}}{n_{0}+n_{1}} \times P_{0} \)
いま\(P_{0}-P\)は蒸気圧の下がった度合いを表し、ΔPとかける。
- また、n0≫n1より \(\frac{n_{1}}{n_{0}+n_{1}}\) ≒ \(\frac{n_{1}}{n_{0}}\)とみなせることから
ΔP= \(\frac{n_{1}}{n_{0}}\times P_{0}\)
いま、溶媒の質量をW0[kg]、溶媒の分子量をM0[g/mol]とすると、
n0=\(\frac{1000W_{0}}{M_{0}}\)[mol]と表すことができるので、代入し、
ΔP=\(\frac{1000W_{0}}{M_{0}} P_{0}\)となる。
ここでn1/W0はmol/kgの質量モル濃度mを表し、\(\frac{M_{0} P_{0}}{1000}\)は溶媒固有の定数であるからkとすると
ΔP=km
となり、蒸気圧降下度が質量モル濃度に比例するということが分かる。
⑹⑺でも似たような議論から似たような式が出てくるので、ここで1回導入しておいた。なおn0≫n1とみなせるほどの薄い溶液でしか成り立たない。
沸点上昇
沸点上昇とは
引き続き水と砂糖水を比べていく。今度は沸点に注目するが、そもそも沸騰というのは温度上昇などに伴い蒸気圧が上がっていき、蒸気圧が外圧に達したところで起こり始める内部からの激しい蒸発のことであった。
いま、水と砂糖水では砂糖水の方が蒸気圧が低くなっているので、当然外圧に達しにくくなっている。そのため沸点が上がる。
このように、溶液の沸点が純溶媒よりも高くなる現象を沸点上昇という。
また、何K(℃)沸点が上昇するかという沸点上昇度Δtは溶液の濃度が薄い希薄溶液の場合、質量モル濃度に比例する。(ラウールの法則参照。n0≫n1の条件を途中で使っているので、希薄溶液でないと成立しない。)
Δt = Kbm (mは質量モル濃度)
比例定数Kbはモル沸点上昇とよばれ、溶媒固有の定数で、問題に与えられる。単位は[K・kg/mol]。
例題
- 水100gにグルコース(分子量180)1.8gを溶かした溶液の沸点は水の沸点に比べて052K高かった。3.0gの尿素(分子量60)を水に溶かした溶液の沸点は何Kか?
【解説】
- 水100gにグルコース1.8g=0.01molを溶かした溶液の質量モル濃度mはm=0.01mol/0.1kg=0.1mol/kgである。Δt= Kbより、
0.052 = Kb × 0.1 ∴ Kb = 0.52K・kg/mol
このKbは溶質によらず水であれば一定であり、いま尿素を溶かした質量モル濃度mは\(\frac{3}{60}\)mol/0.1kg=0.50mol/kgなので
Δt = 0.52 × 0.50 = 0.26K
水の沸点は100℃=373Kより 373.26K
凝固点降下
凝固点降下とは
引き続き水と砂糖水を比較し、今度は液体から固体へ凝固する様子を見ていく。
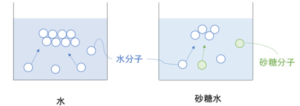
図4
凝固する際には熱運動していた溶媒分子が集まって固体になるが、砂糖水の方では砂糖分子が水分子の集合を邪魔するため、より凝固しにくくなっている。
そのため、砂糖水を凝固させるには純水の時に比べて、より冷やして熱運動を止めてあげないといけない。
このように溶液の凝固点が純溶媒よりも低くなる現象を凝固点降下という。
また、これも沸点上昇の時と同様で、希薄溶液における凝固点降下度Δt[K]は溶液の質量モル濃度に比例する。式としては
Δt = Kfm (mは質量モル濃度)
となり、Kfはモル凝固点降下とよばれ、溶媒固有の定数である。単位は[K・kg/mol]。
例題
- エチレングリコール(C2H6O2)を水2kgに加えて-3.7℃の凝固点とするには、何gのエチレングリコールを加えればよいか?ただし、水のモル凝固点降下を85とする。
- 化合物0.776gをベンゼン10.0mLに溶かした溶液の凝固点は2.46℃であった。この化合物の分子量を求めよ。ただし、ベンゼンの分子量は78、凝固点は5.53℃、モル凝固点降下は5.12K・kg/mol、密度は0.880g/mLとする。
【解答】
- 水の凝固点は0℃なので、Δt = 3.7[K]となる。Δt = Kfmより、
3.7 = 1.85 × m ∴ m = 2mol/kg
よってエチレングリコールは4mol = 62 ×4 = 248g - Δt = 5.53 – 2.46 = 3.07[K]なので、Δt = Kfmより、
3.07 = 5.12 × m ∴ m ≒ 0.600mol/kg
ベンゼンは1mLあたり0.880gなので、ベンゼン10.0mLは8.8gである。0.776g / 8.8g = 0.600mol / kg より、0.600mol ≒ 88.18g
∴ 1mol ≒ 147g
溶液の冷却曲線
引き続き、水と砂糖水を比較し、今度は冷却時間に対する温度変化を図にした冷却曲線の様子を見ていく。
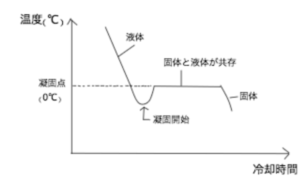
図5
図5が水をゆっくり冷却した時の冷却曲線である。
水の凝固点は0℃だが、実際に冷却していくと、液体の状態のまま0℃を下回ることがある。この現象を過冷却という。過冷却状態を経て水から氷への凝固が始まると、温度は凝固点まで戻り、固液共存状態ままになる。
この、液体から固体へ凝固がすすんでいる間は、液から固という状態変化の際に放出される熱エネルギーと相殺されて、温度は一定のままである。
その後、すべて氷になると以降は温度が下がっていく。
★発展
液体から固体へと結晶化する際には、分子が集まる中心となる核がないといけない。この核を生成するためにはエネルギーが必要であるが、ゆっくり冷却していくとこのエネルギーが得られず、過冷却になってしまう。
そのため、過冷却状態で、振動を与えるなど物理的に衝撃を与えてあげると、一気に凝固がはじまる。
※なお、凝固がはじまった温度は0℃より低いが、これは過冷却の影響によるものであり、凝固点は過冷却が起こらなかった時に凝固が始まる点として定義されているので0℃である。
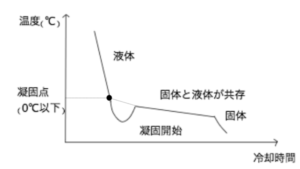
図6
図6が砂糖水の冷却曲線である。水の時との大きな違いは、凝固している最中の固液共存状態でも温度が下がり続けていることである。
これは、水の凝固がすすんでいくと、砂糖水の濃度が濃くなっていき、凝固がすすみにつれ並行して凝固点降下が起こっていくからである。(凝固点降下度Δtはモル質量mに依存)
また、この場合の凝固点は、右肩下がりの凝固点の直線を左に延長し、液体の時の曲線と交わった点になる。
浸透圧
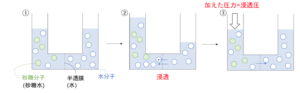
図7
- 図7のように砂糖水と純水を半透膜で仕切られた容器に入れて放置しておく。半透膜というのは溶媒分子を通れるが溶質粒子は通れないほどの小さい穴のあいた膜のことである。液面の高さをそろえておく。
- すると、全体の濃度が均一になるように、水分子が半透膜を通過し、砂糖水の方へ移動していく。この現象を浸透という。
(ナメクジに塩をかけると体内から水分がでてきてひからびてしまうのもこの例)
浸透は砂糖水と水の液面差がある程度ついたことろで止まる。(∵ 重力とのかね合い) - そこで、砂糖水と水を①の時のように同じ液面の高さに戻すためには、砂糖水の側に上から力をかけてあげなければいけない。
その圧力のことを浸透圧という。
これは意味としては、濃度を均一にしようと溶媒が半透膜を通過しようとする②の圧力のことと同じである。
溶液の濃度が濃ければ濃いほど、半透膜が通過しようとする浸透圧も大きく、また温度が高ければ高いほど熱運動が激しくなって浸透圧も大きくなる。
この浸透圧Πは希薄溶液では、
Π=C・R・T(Cはモル濃度。Rは気体定数。Tは絶対温度)
という式を満たし、
これはファントホッフの式と呼ばれている。
※Cは質量モル濃度ではなくモル濃度であることに注意。
C[mol/L]=\(\frac{n[mol]}{v[L]}\) と表せるので、Π=\(\frac{n}{v}\)RT↔︎Πv=nRTとなって理想気体の状態方程式と同じ形になる。
- Ex) ある非電解質の固体の質量14gを水に溶かして100mLにした水溶液の浸透圧は27℃で8.31×104paであった。この試料の分子量を整数値で求めよ。
Π=CRTより、8.31×104=C×8.31×103×300 ∴ 0.033mol/L
いま、1.14g/0.1L=0.033mol/Lより、0.033mol=11.4gなので1mol=342g
電解質溶液の性質
いままでは水と砂糖水という比較で見てきたが、砂糖水の代わりに食塩水を用いると、少しだけ注意が必要である。
この2つの違いは、砂糖水は砂糖分子(グルコースなど)が電離しない非電解質溶液であるのに対し、食塩水はNaClが電離する電解質溶液になっている点である。
ここまで見てきた、蒸気圧降下、沸点上昇、凝固点降下、浸透圧はいずれも、溶液の中にどのくらい溶質の粒子がとけているかが大切であった。
そのため、NaClのように電離するものに関しては、NaClを0.1mol溶かしたとしても、Na+0.1molとCl–0.1molになるので2molの粒子がいるとして濃度計算をしなければならない。(逆に、溶媒中で2分子が結合して二量体を形成するものは、粒の数が減ったものとして計算する。)
- Ex) 涙や血液とほぼ同じ浸透圧を示す、90%のNaClaqは生理食塩水とよばれ、傷口の洗浄に用いられる。生理食塩水の密度は1.0g/cm3、Na=23、Cl=35.5とすると、体温(37℃)での浸透圧は?
NaClaq0.90%では、NaClaq1L中に9.0gのNaClが含まれているので、
C = \frac{9}{58.5}mol/L ≒ 0.154mol/Lである。いま、水溶液中では完全電離するため、
粒子の濃度は2 × 0.154 = 0.308mol/Lとなる。よって Π=CRTより
Π=0.308×8.31×103×310
=7.9×105pa
コロイド溶液とは…?
直径が10-9~10-7m(1~100nm)程度の大きさで分散している粒子のことをコロイド粒子という。
コロイドは、適度に大きく、10-9mより小さいと分子た原子のサイズであり、10-7mよりも大きいと沈殿してしまうので、分散するには良い大きさである。イメージとしては「にごり」のこと。
Ex)
- 固体中のコロイド→マシュマロ、ゼリーなど。
これらは流動性がなく、ゲルと呼ばれている。 - 液体中のコロイド→牛乳、絵の具、マヨネーズなど。
これらは流動性があり、ゾルまたはコロイド溶液と呼ばれている。 - 気体中のコロイド→雲、煙など。
ゾルを室温で放置しておくと、水分が抜けていき、ゲルになって、さらに完全に水分が抜けたものはキセロゲルと呼ばれる。
コロイド粒子は一定の符号の電荷を帯びており、コロイド同士が互いに近づくことがない(同符号なので)ため、沈殿しないでコロイド状態を保っていられる。
コロイド溶液の性質
- チンダル現象
コロイドはその大きさが光の波長と近いために、よく光を散乱させる。そのため、レーザーなどの強い光線をコロイドに当てると、光の道筋が明るく輝いて見える。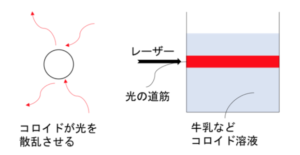
図8
これをチンダル現象といい、限外顕微鏡などに用いられている。 - ブラウン運動
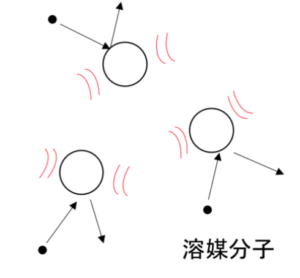
図9
コロイド粒子は観察するととても不規則にふるえて運動している。これをブラウン運動という。
溶媒分子が熱運動により動き回っており、それがコロイド粒子にたえず衝突することで、コロイド粒子自身も不規則な動きをしている。 - 透析
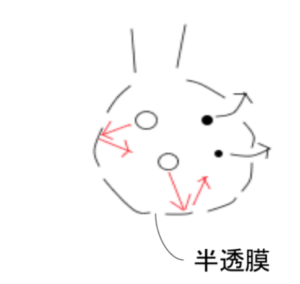
図10
コロイド粒子は大きいので、ろ紙の穴は通れるが、半透膜の穴を通過することはできない。これを利用すると、コロイド溶液から不純物の分子のみを取り除き、精製することができる。
これを透析という。腎臓のはたらきが低下してしまった際に、外的手段で血液から老廃物を取り除く、人工透析はまさにこれである。 - 電気泳動
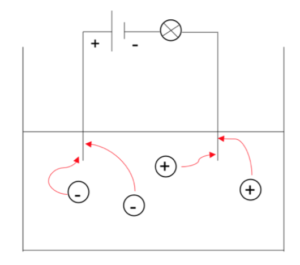
図11
コロイド粒子は電荷をおびているため、直流電圧をかけると-のコロイドは+極へ、+のコロイドは-極へと移動する。これを電気泳動という。 - 凝析

図12
コロイドは+または-の電荷をおびているため、互いに近づけず、沈殿しないわけだが、そのコロイドと逆の符号のイオンを加えてあげると、たちまちにくっついて大きくなって沈殿する。
このように少量の電解質溶液に加えてあげることで、コロイドを沈殿させることを凝析という。+もしくは-の電荷の数が大きいほど、凝析しやすい。
Ex) Fe(OH)3というコロイド溶液は+に帯電している。これを凝析させるにはNaClよりも MgOの方が有効である。(Clは-1、Oは-2) - 塩析(親水コロイドのみ)

図13
コロイドの中で親水力が大きく、多数の水分子は水和して存在しているコロイドを親水コロイドという。
水和されているので、電荷の影響を受けにくく、少しの電解質を加えても凝析しないが、大量の電解質を加えると水分子が離れて沈殿する。
これを塩析という。 - 保護コロイド(親水コロイドのみ)
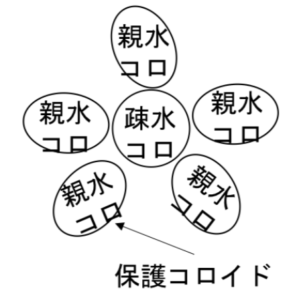
図14
コロイドの中でも水との親和力が小さいものを疎水コロイドという。
疎水コロイドは水とあまり触れあいたくないので、親水コロイドが共存していると、親水コロイドが疎水コロイドを取り囲んで、凝析されにくい状態にする。
これを保護コロイドという。