本記事は カレンダー と年月日に関する問題を集め,それらの解説をしていくものです。これらと中学受験に何の関連があるのか?と疑問に思われた方もいると思いますが,実はカレンダーや月日のような規則的な数字の並びは,実は問題にするのにぴったりなのです。
実際標準的な学校から難関校まで様々なレベルの算数の問題で,日付と関連するものが出題されています。いろいろな規則性の問題に慣れるという意味でも,触れた方が良いことは間違いありません。今回は初めに出題されがちな規則について触れ,その後いくつかの問題をピックアップし解説をしていきます。


Contents
カレンダー ・日付で覚えておきたい要素
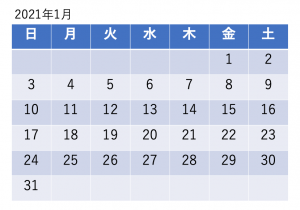
ではカレンダーの数字の並びにはどのような規則があるのでしょう。以下では今年2021年1月のカレンダーを参考にして,様々な規則について見ていきます。
縦のラインについて
まず縦のラインの数字に注目しましょう。日曜であれば3・10・17・24・31,月曜であれば4・11・18・25と数字が並んでいます。この数列からも分かる通り,数字が7ずつ増えています。1週間=7日なので当然なのですが,意識してこの縦のラインの差を考えることが問題を解く上で大切になってきます。
横のラインについて
次に横のラインについて注目します。例えば2列目は3・4・5・6・7・8・9と1ずつ増えています。これも縦のラインの規則性と同様,当然ではあるけれども受験に出てきたときには意識的に考えなければいけないことです。
そしてこの1ずつ増えているという規則に関連することですが,カレンダーは7つの曜日で構成されているため,各曜日について7で割ったときのあまりは7通りになっています。例えば先ほどのカレンダーの2列目の数字を7で割ってみると,
3・4・5・6・0・1・2
となっていますね。続いて3列目を7で割ってみましょう。
3・4・5・6・0・1・2
2列目と同じ値が出てきました。このように横のラインで見た時に7で割ったあまりは7通り現れ,日曜はあまりが3・月曜はあまりが4・・・という規則が見出せます。この規則は月ごとに異なりますが,ある月の中で曜日が同じであれば,あまりが等しくなるという関係は覚えておきましょう。改めて7で割ったときのあまりについてカレンダーを作成してみます。
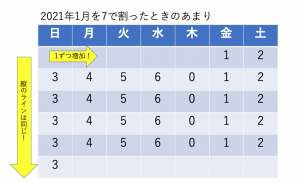
この縦の+7という増加・横の+1という増加に注目すると,例えば斜めのラインでは数字と数字が8離れているということや,2個下の数字は14離れているということも分かります。様々な規則性を見出せますが,基本となるのは縦と横の増加です。覚えておきましょう。
各月を構成する日数
ここからはそれぞれの月を構成する日数について考えていきましょう。1月は31日で構成されています。しかし1月以降も同じように31日で出来ているわけではありませんよね。2月は28日,3月は31日,・・・で構成されています。
この日数を把握しておくことも中学受験においては重要です。中学入試の算数の出題範囲には日暦算があります。これは○月×日の△日後はいつですか?というものですが,このような問題を解く上で30日か31日かということを正確に覚えておかなければなりません。
まずそれぞれの月には31日で出来ている大の月とそれより少ない日数で出来ている小の月とがあります。小の月でないものが大の月なので,小の月の一覧を知っておけば大丈夫です。
具体的には28日しかない2月と30日しかない4月・6月・9月・11月とが該当します。2・4・6・9・11の語呂合わせで西向くサムライと覚えておくとよいでしょう。11 がサムライになるのは,漢字の十と一を組み合わせたら武士の士,つまりサムライという意味の漢字になるからです。

うるう年について
そして日暦算の特殊なパターンを対策するために,うるう年についても確認しておきましょう。特殊なパターンとはうるう年をまたぐものです。先ほどの○月×日の日暦算の例は,ある月の日付と別の月の日付との間を考えるものでした。しかし日暦算はこれだけでなく,ある年の日付と別の年の日付とがどれだけ離れているか,について計算させるものもあります。例えば2017年→2020年のようにうるう年をまたいでいるものは,2016年→2019年と同じように考えると正しく計算できません。
したがって4の倍数年であるうるう年には2月29日があることを忘れてはならず,計算するときに多くカウントしなければならないということを覚えておきましょう。ちなみにうるう年でない年のことを平年と言います。このことも頭の片隅に入れておいて損はないでしょう。
カレンダー に関する問題を解いてみよう
ではここからはいくつか上の知識を使った問題をご紹介いたします。簡単なものから少し難しいものまでの計3問を引用しています。よろしければまずは自分の力で一度解いてみて,その後にそれぞれの問題の下に続く答えを見てみてください。良い演習の機会になると思われます。
問題1:日暦算
まずはすぐ上で登場した日暦算について挑戦してみましょう。
ある年の2月5日は金曜日でした。この年の8月12日は何曜日でしょう。ただし,この年はうるう年でないものとする。
解説
ここからは1問目の解説に移ります。この問題で聞かれているのは何曜日か,ということですね。前述の解説で,ある月の同じ曜日であれば,その日付を7で割った時の余りが共通しているということをご紹介しました。この性質を使って解いていきます。
いま2月5日が金曜日であるという条件が提示されていて,5を7で割ったときのあまりは5になります。それゆえ2月の日付を7で割ったときのあまりが5であれば金曜日,続けてあまりが6であれば土曜日,あまりが0であれば日曜日,・・・という関係が導かれます。

しかし今回比較するのは8月です。ある月と別の月とで日付を7で割ったときのあまりが共通しているとは限りません。そのため8月12日が2月何日に相当するか,を考えていく必要があります。
そのためまず2月5日と8月12日が何日間離れているかを考えていきます。まず「日」が同じ8月5日が2月何日に当たるかを計算します。まず3月からです。この年は平年であり,2月は28日あるため,3月5日は5+28=33日,つまり2月33日に相当します。
4月5日についても同様に考えましょう。3月は31日あるため,4月5日=3月5+30日=2月5+28+31=64日,つまり4月5日は2月64日と言い換えることができます。
このように実際に存在しない日付を考えていくことが日暦算では有効です。続けて4月は30日,5月は31日,6月は30日,7月は31日であることを踏まえてこれらの数字を足していくと,
8月5日=2月(5+28+31+30+31+30+31)=2月186日
となります。10月5日の7日後が10月12日なので,10月12日=2月186+7=193日と言い換えられます。ここから,193を7で割ったあまりを算出し,先ほどの2月の曜日とあまりの関係に照らし合わせれば,8月12日が何曜日か分かるという見通しが立てられます。
193÷7=27あまり4
であるため,10月12日は2月のカレンダーの中で,7で割ると4あまる曜日に該当していると分かるわけです。ここで,上で確認した2月の曜日とあまりとの関係を見ると,4あまる曜日は木曜日なので10月12日は木曜日となります。
A.木曜日
問題2: カレンダー をまるで囲む問題
ここからはカレンダーについての問題をご紹介いたします。まずはいくつかの日付を丸で囲む問題です。
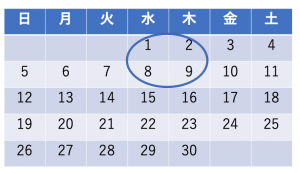
下の図のように,カレンダーでたて・横それぞれ2列ずつ,計4つの数を囲みます。例えば次のように4つの数字を囲むと,それらの数字の合計は20になります。いま囲んだ4つの数の和が44になったとき,カレンダーのどの部分が囲われているでしょうか。
解説
それでは解説をして参ります。ここで考えるべきなのは4つの数字の関係です。
試しに例としてカレンダーに提示されている4つの数に注目してみましょう。左上の数字が1になっています。1の右が2,下が8,右下が9です。これらの数字の差を考えると, 4つの数は,
左上の数,左上の数+1,左上の数+7,左上の数+8
で構成されていることが分かります。このときもちろん右上を,左下を,右下を中心に考えても問題ないです。やりやすい場所から考えをスタートして,問題を解いてみてください。今回の問題であれば,左上の数が分かれば囲いの中の4つの数が全部分かるということが分かります。そしてこれらの数字の和を考えていきましょう。足したら44になるときの囲いの左上の数を□とすると,4つの数は次のように表されます。
□,□+1,□+7,□+8
そしてこれらの数字を全て足すと,
□+(□+1)+(□+7)+(□+8)=□×4+16
となります。よって□×4+16=44を満たす□の中に入る数字を考えていけばいいですね。
□×4+16=44
□×4=28
□=7
このことから囲いの左上の数は7だと分かりました。あとは7に1加えた数,7加えた数,8加えた数を考えていけば囲いの全ての数を求められます。
A.7・8・14・15
問題3: カレンダー から選択する問題
最後の問題は同じくカレンダーと関連する問題です。この問題は実際の入試で出題されたものです。そのため今回の3問の中では最も取り組みづらいかもしれませんが,上に記載されていることを見ながら取り組んでみてください。
次の①・②・③に当てはまる言葉または数字を書き入れなさい。
下の表はある月のカレンダーです。この月のア〜オの各週から1つずつ,全て異なる曜日の5日を選んでそれぞれ丸で囲みます。丸で囲んだ5つの数の和が81になるのは,①曜日と②曜日の2つの曜日を除いた5つの曜日から5日を選ぶときです。ただし,①,②の順序は問いません。そして,丸で囲んだ5つの数の和が81になる選び方は全部で③通りです。
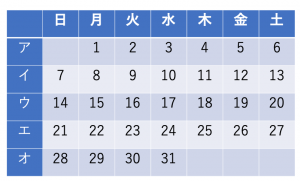
(灘中学校(2017),一部改題)
解説
ここからは3問目の解説をしていきましょう。
まずア~オの列に存在する数字の性質について見ていきます。アの列は1~6ですね。イの列は7~13ですが,これは上の解説で述べた7で割ったときのあまりから考えると,7+アの列の数と言い換えることができます。ウの列についても同様に言い換えると,14+アの列の数と表せます。このようにしてエの列・オの列についても同じように表しましょう。
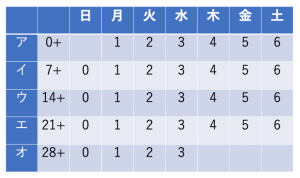
ではこの+7ずつの縦の増加と各曜日とあまりの関係が何の役に立つのでしょうか。問題では5つの数をそれぞれの列から選びなさいと指定されていました。このとき上の表を使うと,ア~オから数を選んで和を求めるとき,次のように書き換えられます。
アの数+イの数+ウの数+エの数+オの数=(0+7+14+21+28)+(0~6のあまりのうち5つ)
=70+(0~6のあまりのうち5つ)
ここでいま,5つの数を足したときの合計が81になることから,あまりを5つ足したら81-70=11になるということが分かります。
0~6までの全ての数を足すと21になるので,足したら10になるように2つの数字を選んで除けばいいですね。この中で2つ足して10になる数字は4と6の組しかありません。よってあまりが4の曜日と6の曜日,つまりは木曜日と土曜日を取り除けばいいと分かります。よって①・②に当てはまる答えは木曜・土曜となります。
では最後に5つの数の選び方を検討しましょう。この選び方の数は少々難解かもしれません。その難しさは金曜日がオの行に存在しないこと,日曜日がアの行に存在しないことが関連しています。そのため分かりやすく計算できるように,日曜日がアの行にも存在すると仮定して,そのときに算出した場合の和からアの行の日曜日を使ったものを引いていく,という手順で求めていくことにします。金曜日がオの行に存在すると仮定してもいいですね。

まず上の図でいう左のときの場合の数を求めていきます。初めに数が一つ少ない金曜日についてですが,これはア〜エの4行に存在しています。このことから金曜日の振り分け型は4通りです。残った振り分けた行以外の4列には,金曜日以外の4行を振り分ければいいですね。したがってこのときの場合の数は,次のようになります。
4×4×3×2=96
次に上の図でいう右のとき,つまり存在しないアの行の日曜日に丸をつけるときの場合の数を求めていきます。このとき他の曜日と違ってイ〜オの3行にしか存在しない金曜から考えていきましょう。金曜日は3行のいずれかに振り分けられます。残った月曜・火曜・水曜を金曜で選んだところ以外の3行に振り分けていくことで,場合の数は次のように求められます。
3×3×2=18
このことから96-18=78と計算でき,よって丸で囲んだ5つの数の和が81になるような数字の選び方は78通りとなります。
A.木,土,78
まとめ……の前に
登録6000人以上! 本サイト、中学受験ナビの監修も務めている『開成番長』こと繁田和貴が執筆する完全無料のメールマガジンでは、主に中学受験生のお子さんをお持ちの方へ向けた様々なお役立ち情報を配信中! さらに今なら登録者にはもれなく「開成番長・繁田の両親が語る繁田の中学受験PDF」をプレゼント! 登録及び登録解除も簡単ですので、お気軽にご登録ください。

まとめ
ここまで中学受験で問われるカレンダーや月日についての知識と,それらが絡む算数の問題の演習と解説を扱ってきました。前半の知識部分については当然のことが多いようにも思われますが,このような自明のことを意識して問題を解いていくことが重要,という意味でご紹介いたしました。後半で引用した問題に関しては,これらのパターン以外の規則や計算が求められることもあるので,ご自身で更なる対策を行なって頂ければと思います。本記事が学習の参考になれば幸いです。
(ライター:大舘)


















