今回の記事は還元算・相当算についてのシリーズの第3本目の記事となっています。初級編では□のある計算方法などについて,中級編では線分図を書くという文章題を攻略する際のテクニックについて説明していきました。今回は入試問題なども引用しながら,実践的な考え方をご紹介していきます。よければ一読してみてください。
還元算・相当算のポイントは?中級編のおさらい!
まず上級編の本題に入る前に,前回の中級編で確認した還元算・相当算を解く上で注目すべきポイントについておさらいしていきましょう。還元算・相当算の文章題には,ある重要な特徴がありました。それが2つの基準があるということです。
2つの基準とは例えば,数字と割合であったり道のりと速さであったりを指します。このような2種類の異なる指標によって1つの事柄についての情報が与えられている,というのが還元算・相当算の基本でした。今回出てくる問題にもきちんと2つの基準が存在していますので,その点に着目して問題を分析することから始めていきましょう。
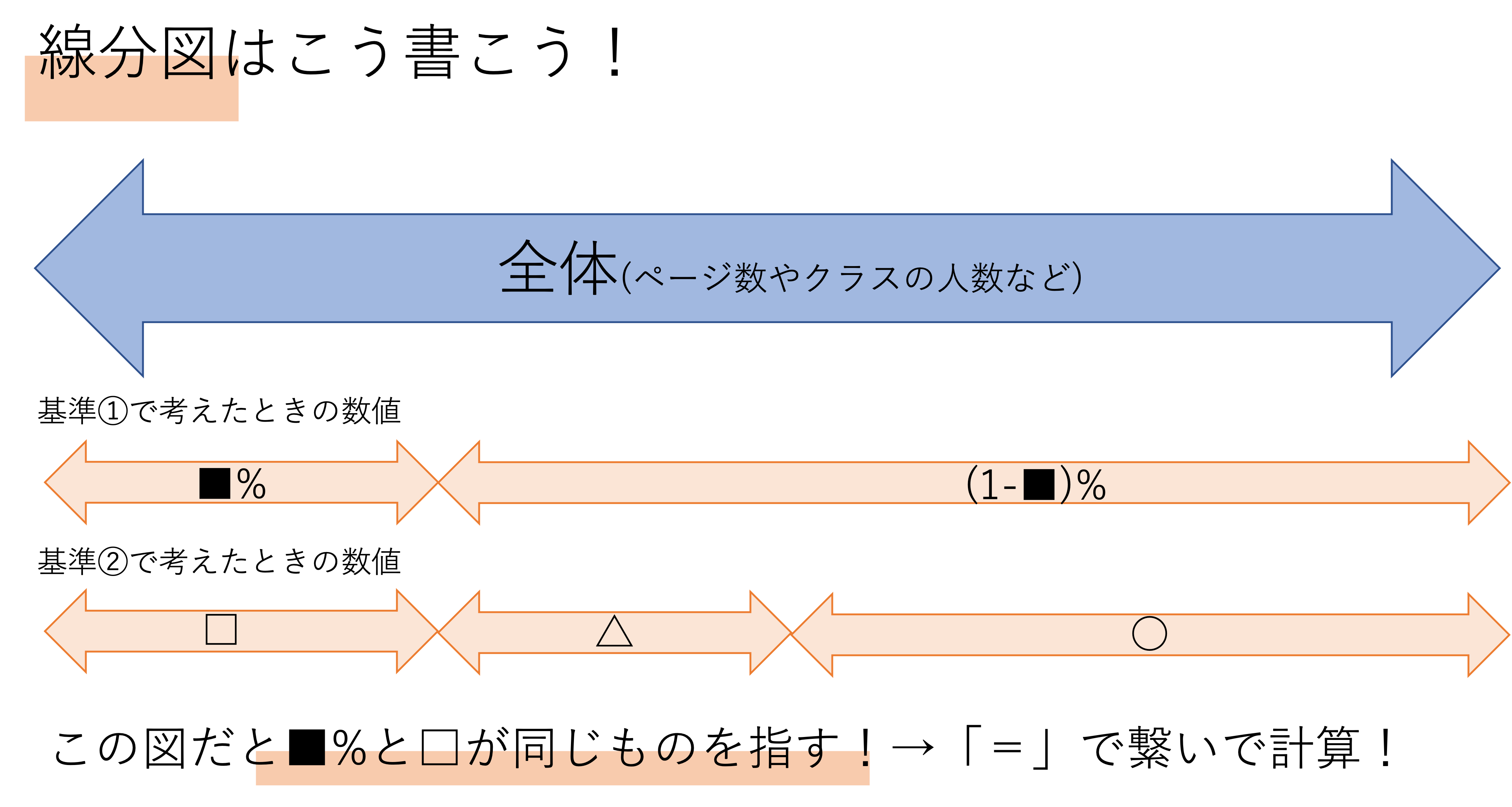
そして2つの基準があるということから,それらの基準を整理する線分図という攻略法が有効にはたらくことも解説していきました。線分図の書き方はこれから引用する問題の解説でもご紹介しますが,基本は全体の量を1として線分に表すことから始めていきます。そうして出来た線分図のうち,基準は異なるけど指しているものは一致している部分を探すのでしたね。忘れてしまった人は一度中級編に戻ってみてもいいでしょう。
問題を解いてみよう!前編
まずはウォームアップとして,前回の中級編でも出題したような基本的な還元算・相当算を解いていきましょう。比が出てくるのでやや解きづらいかもしれませんが,じっくり考えてみてください。
次の□の中にあてはまる数を入れなさい。
AとBが持っているカードの枚数の比は5:2です。BがAにカードを4枚わたすと持っているカードの枚数の比が11:4になります。2人が持っているカードの枚数の合計は□枚です。
(青稜中学校(2018),一部改題)
解説
それでは解説に移ります。無事解けた人も答えが怪しい人も全く解けなかった人も,ぜひ回答を見ながら攻略のポイントを一緒に抑えていきましょう。
まずはこの問題における2つの基準とは何か・全体とは何かということを,問題を眺めながら考えていくといいでしょう。今回は還元算・相当算としてこの問題を引用していますが,受験本番で「これは還元算・相当算です」などと示されるわけではありませんよね。そのため日頃から問題の特徴には注意しておくといいでしょう。
さて,この問題ではカードの枚数についてのことが書かれています。そして求めたい答えがカードの枚数の合計であることからも分かる通り,2人が持っているカードの枚数を1として答えを考えていけば今回は正解にたどり着けそうです。そしてこのカードに関する2つの基準ですが,問題文では枚数と比というものが与えられていますね。このうち枚数については「4枚」という記述しかないのですが,それでも大事な情報です。
このようなことが確認できたら,次は線分図の作成に移りましょう。今回の問題を図に整理すると次のようになります。このとき,2つの基準ということに注目しようと先程説明しましたが,シチュエーションの変化について考えていくことも大切です。例えば今回はカードをAさんがBさんに渡すというイベントが発生しているので,交換前と交換後という2つの場面が考えられますよね。さらにはそこで生まれた差というところにも注目できるようになるので,図にまとめるのが難しかったかと思われます。是非悩んでしまった人は下の図を参考にして図を作る,ということを覚えておきましょう。
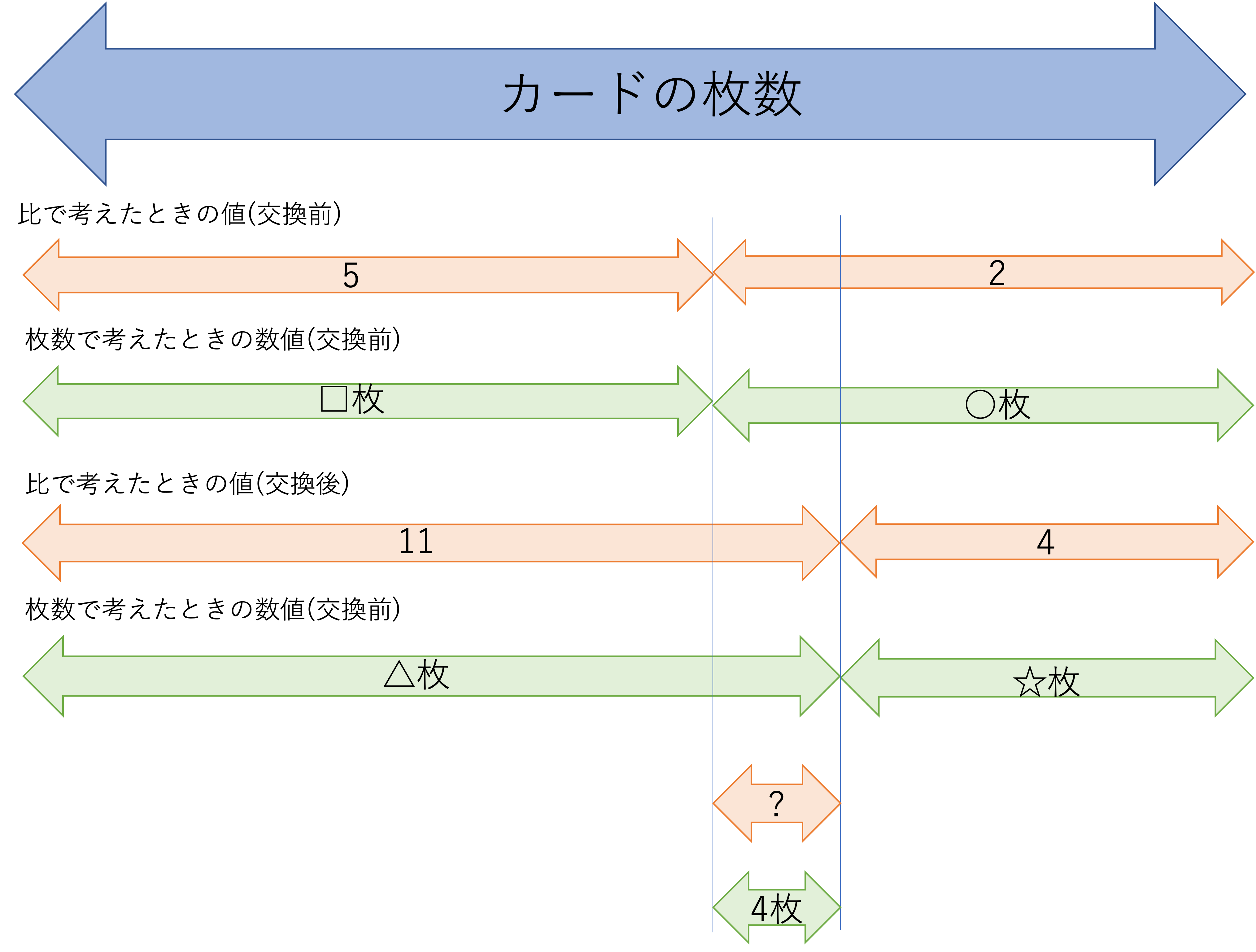
そして今回は枚数についての値が,交換した前と後で4枚違うという指示しか出ていなかったので,この違いに注目して問題を解いていきましょう。差の部分の比は問題文に出ていませんでしたが,それは交換前と交換後の値を比較することで導くことができそうなので問題ありません。このように図にまとめると,どこから解くのが近道なのかということまでハッキリとしてくるので,その点でも攻略に大変役立ちます。
ではこの交換前と交換後の差に着目して,異なる2つの基準で測ったとき,その値がどのように表されるかを考えましょう。まず枚数の差はわかりやすいですね。問題文で4枚という指示があったので,その値がちょうど使えます。
それでは比の差・割合の差について考えていかなければいけないのですが,比の引き算を考えるには比の全体を揃えなければいけないということをつい忘れてしまいがちです。例えば今回は5:2,11:4という比が登場していますが,2つの比の全体はそれぞれ7と15ですよね。そのため,5:2という比の中の「1」が表す量と,11:4という比の中の「1」が表す量が変わってきてしまうのです。そのことを解決するために,比の分母を揃えてから計算をするというわけです。今回は7と15の最小公倍数が105なので,全体が105になるように比を揃えてあげましょう。
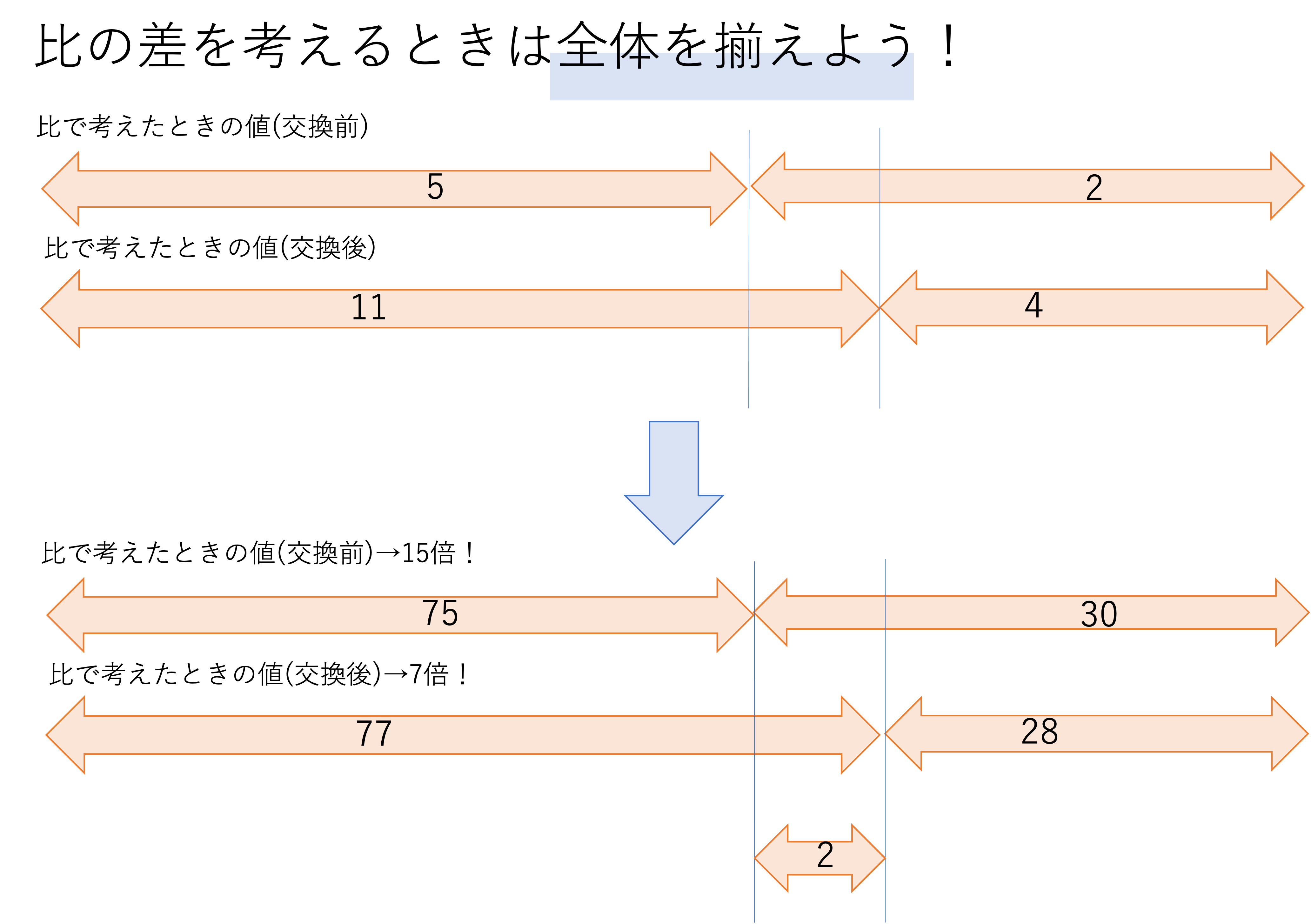
このようにして考えると,比で交換前と交換後の差を表したら2になることがわかります。この2という数字は105という全体のうちの2を指すので,その点には注意が必要です。つい%で考えてしまって,100が全体だと捉えてしまいがちです。気をつけましょう。
さて,こうして交換前と交換後の差を表す2という比の量と4枚という枚数の量が求められたわけですが,この2つの数値から,カードの枚数全体を105と見たときの1が2枚に相当することが分かります。そして今回求めるのはカード全体の枚数だったので,
比率:枚数=1:2=105:210
という関係から答えは210枚になります。
A.210枚
いかがでしたでしょうか。比の計算の仕方や分母・全体を揃える,というテクニックを知らないと解きづらい問題でしょうが,還元算・相当算という文章題そのものはそこまで難しくない,ということがお分かりいただけたら幸いです。
問題を解いてみよう!後編
続いても青稜中学校からの出題です。こちらはシンプルな問題文ですが,どこから手をつけていいのか分からないと悩んでしまうかもしれません。基本に忠実に,を意識して月校考えてみるといいでしょう。
次の□の中にあてはまる数を入れなさい。
あるクラスの生徒の40%は女子で,男子と女子の人数の差は7人です。このクラスの男子の人数は□人です。
(青稜中学校(2016),一部改題)
解説
まずは1問目と同じように,全体を指すものは何か・2つの基準にはどんなものがあるのか,を考えていきましょう。今回の文章題ではクラスの人数が話の中心になっています。そのためクラスの人数が全体に相当するのではないか,と予測できますね。そしてクラスの男子と女子に関して,人数と割合という異なる基準から情報が与えられていることから,この問題を分析していくと次のような線分図がおこせます。
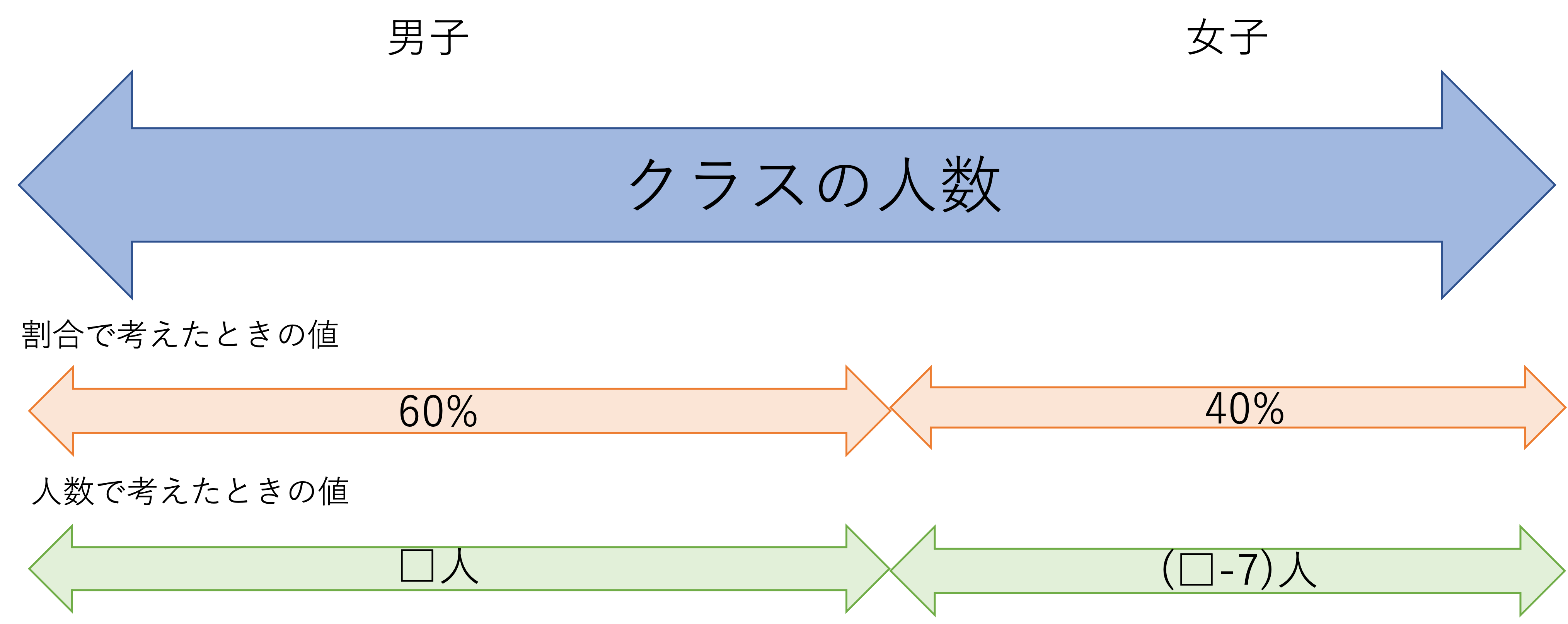
この図を見つつ,問題文で与えられていた男子と女子の人数の差が7人という要素に焦点を当てて答えを考えていきましょう。この男子と女子の差は人の数という基準で見ると7人だと説明できますが,もう片方の割合という基準で考えたときの差はどれくらいでしょうか。割合で考えたときの差は,女子の割合が40%・男子の割合が60%であることから,20%であると計算できますね。このようにして考えると,男女間の差は,20%という割合と7人という人数とで説明できることがわかります。そしてこれらを比の関係に整理すると,
割合:人数=20%:7人=40%:14人=60%:21人
という式が成立することになります。そしてこの問題で求められているのはクラスの60%を占める男子の人数だったので,答えは21人となります。
A.21人
いかがだったでしょうか。この問題は1問目に引き続き,線分図が書けたか書けなかったかが正しい解答を導けたかどうかに大きく関わってくるものだったと思われます。慣れてくれば線分図も簡単に書けるようになりますので,もし間違えてしまってもいっぱい対策を重ねればいつの間にか攻略できるようになるでしょう。
まとめ
今回は入試に出題された問題に挑戦してみようという趣旨で,還元算・相当算の取り組み方をご紹介していきました。今回使った線分図というテクニックは,前回の記事で詳しく解説していますが,これはどんな文章題に対しても使えるものです。この記事はもちろんのこと,以下の参考文献やおすすめ記事なども活用しながら身につけていきましょう。本記事が今後の学習の参考になれば幸いです。


















