今回は 比の性質 について解説していきます。日常生活の中でもしばしば「比」というものを耳にするかと思われますが,中学受験に挑むにあたってもこの比の性質というものに対する理解は必須です。今回は基礎編として,比の特徴を簡単にご紹介していきます。低学年のお子様でも分かりやすい内容にまとめていますので,よければ参考にしてみてください。
Contents
比とは?
まず比とはどんなものを指すのでしょうか。知っている人もいるかもしれませんが,改めて振り返っておきましょう。あまり詳しくない人は,ゆっくり読み進めながら理解を深めてみてください。
簡単に言ってしまえば,比とは比率の表し方の1つです。普通,割合と言われたら片方が他方の30%だとか,3倍だとか,1/3のように表す方法を考えるかと思います。この表し方は,片方を基準としてもう片方を表すと言う方法です。言い換えると,あるものが全体のうちに占める量を表しているのが割合,とも言えるでしょう。それに対して比というものは,基準を設けずに,別の言い方をすれば2つの数値をそのままに関係として整理した比率を指します。
ちなみに比の式の書き方・表し方ですが,比の式は2つの数を左右に並べて間に「:」というマークを書いて繋げることで完成します。この「:」というマークは「たい」と呼び,例えば2:3という式は「に たい さん」と呼びます。覚えておきましょう。
比の長所!
しかし,表し方が違うだけで何が変わるのでしょうか。例としてここに12個のアメと18個のクッキーがあるとして,関係の整理の仕方を見ていきましょう。この2つの数量の関係をこれまで習ってきたような割合で表すとするとどうなるでしょう?おそらくは片方を1として計算することになるかと思われます。例えば,アメを1とするとクッキーはアメの150%もしくは1.5倍ある,などと説明するでしょう。ただしこれでは計算が面倒ですし,実際150%の個数,と言われてもピンと来ないところがあります。
それでは,この関係を比で表すとどうなるでしょうか?上の書き方・表し方で確認したような手順でこの二つのお菓子の数の関係をまとめると「12:18」となりますね。この表し方が便利なのは,数を直接比較できる点にあります。それ以外にも後述するように,変形してわかりやすい形にできるという長所もあります。このような考え方・長所の違いを頭に入れておくと,この先の内容も分かりやすくなるかもしれません。
比の3つの性質!
それではここからは比に存在する3つの特性についてご紹介していきます。
比は分数で書き換えられる!
重要な要素の一つ目が,比は分数に置き換えられるということです。これは,比は割合の形に変換できる,とも言い換えられます。「どういうこと?」と思われるかもしれませんが,まずは作り方を覚えてしまいましょう。比を分数に直すには,「:」の部分を「/」と書き換えてあげればいいだけです。
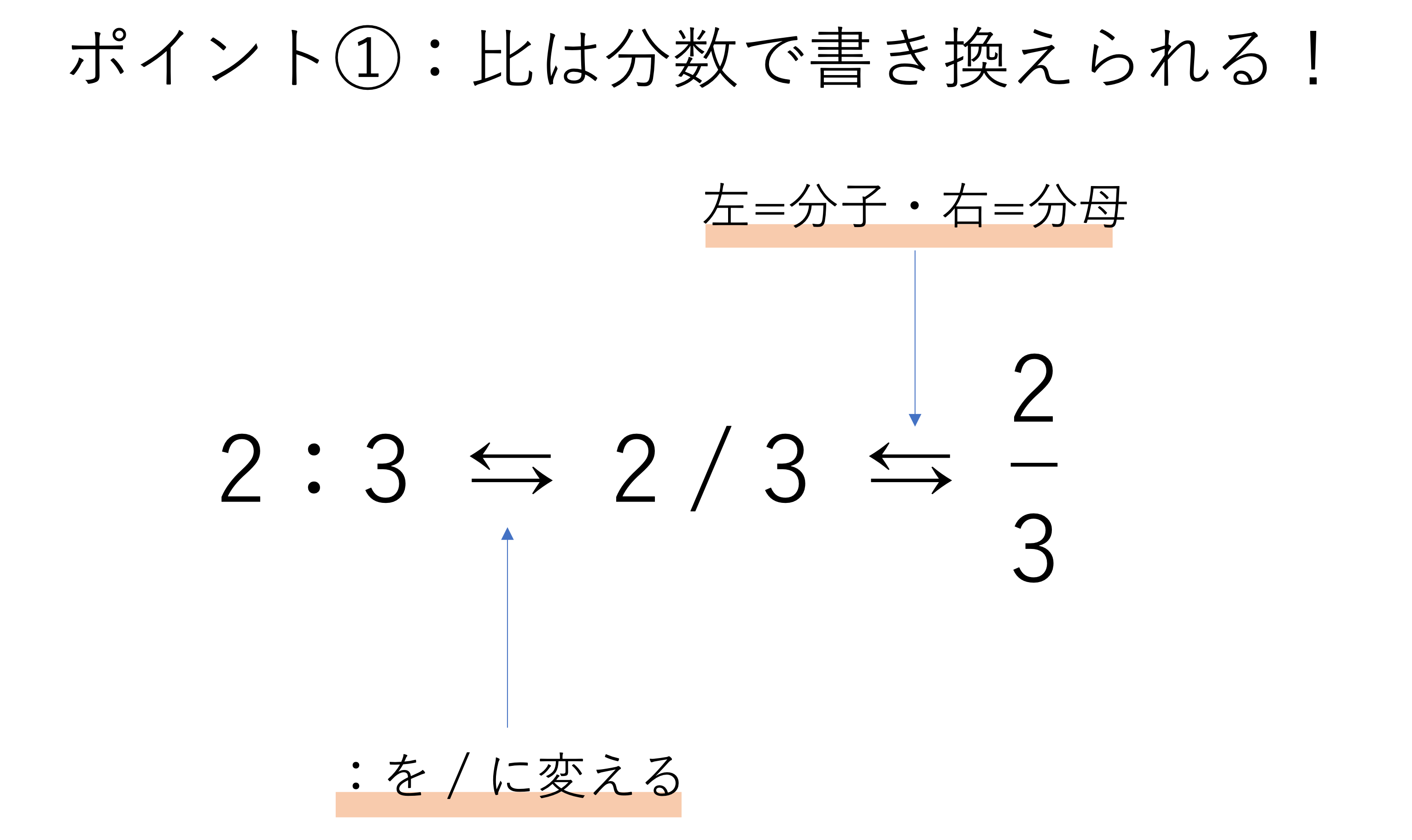
この分数は一体何を表すのかというと,比の式で右側の数字を1としたときに左側の数字がどれくらいを占めているかという数値になります。これはつまり,右の数字に対する左側の数値の割合と同じ意味ですよね。これが前述した「比は割合の形に変換できる」の意味です。
そして裏を返せば,これは割合の数字を比に置き換えられるとも言えます。分数の分子と分母を分子:分母の形で表せば,分子と分母の数量の比を作ることができます。このような書き換えは色々な場面で有効です。頭に入れておきましょう。
比はかけたり割ったりできる!
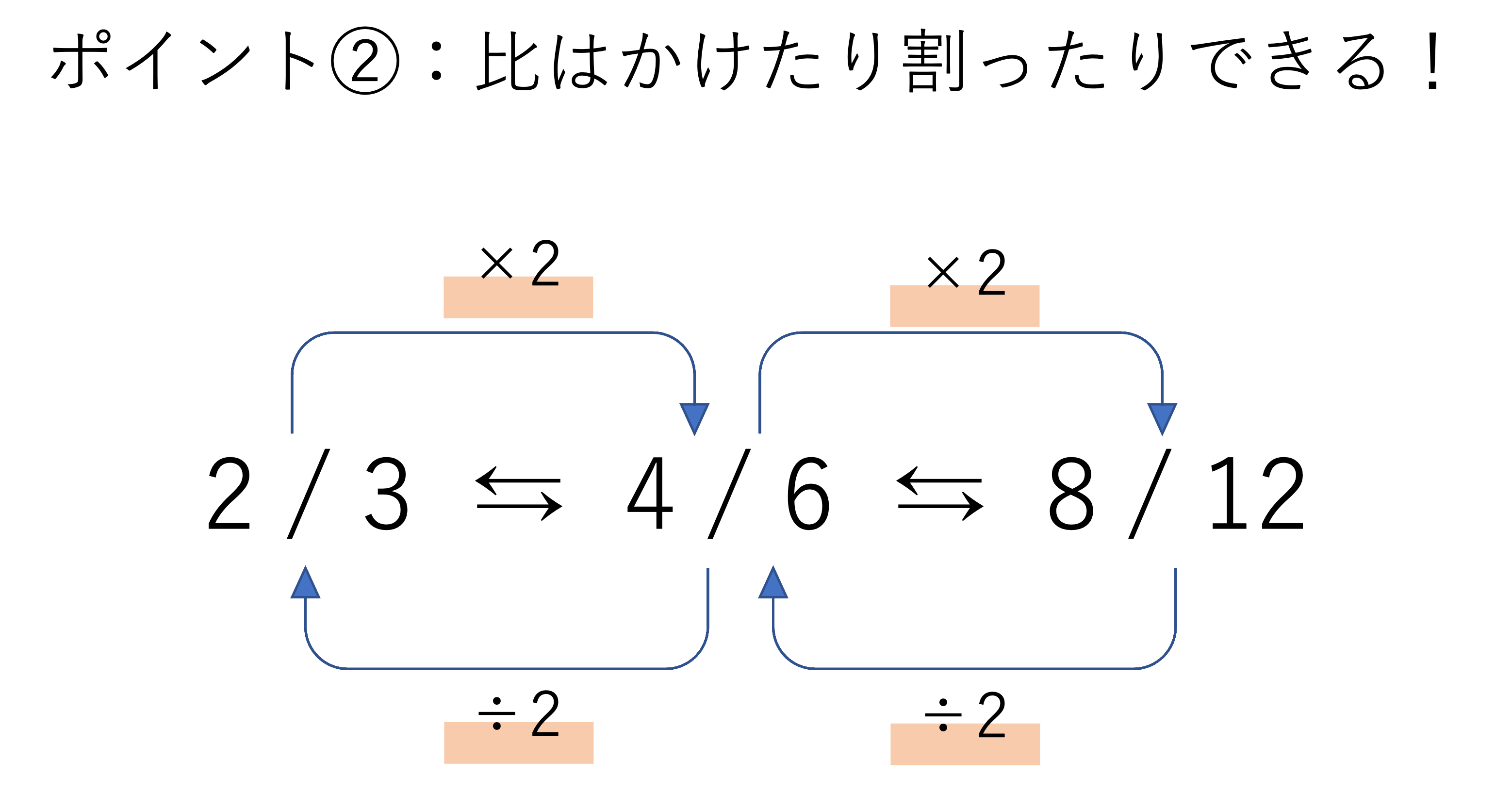
続いて覚えておきたい特徴が,比はかけたり割ったりできるということです。先程上の章で,比は分数と同じようなものだという説明をしましたね。そしてここで思い出して欲しいのが,分数は分母と分子に同じ数をかけたり同じ数で割ったりしても値が変わらないということです。これと同じ性質が実は比にも存在するのです。
例えば4:6という比があったとしましょう。これを分数で表すと4/6=2/3となるわけですが,この比の左と右に2をかけてみたらどうなるでしょうか。8:12という新しい比ができますね。しかしこの比を分数で置き換えてみると8/12=2/3になり,先ほどみた分数と値が一致しますよね。このことから次の関係が成立するというわけです。
4:6=4×2:6×2=8:12
また4:6の右と左を今度は2で割ってみましょう。割り算をすると新たに2:3という比が生み出されますが,これを分数に直すと2/3となり,やはり先程の値と一致しますよね。このことから次の関係も成立すると言えます。
4:6=4÷2:6÷2=2:3
このように比には両辺をかけても割っても値が変わらない性質があります。そしてこの性質を使って,数が大きい比や小数・分数が使われている比を,それ以上小さくできない整数の比で表すことを「簡単にする」と言います。色々な問題で見かける単語だと思うので,覚えておきましょう。
比の等式はかけ算で整理できる!
最後にお伝えしたい特徴が,比の等式がかけ算で整理できるということになります。まず等式とは,2つの数が「=」で結ばれた式のことを指します。このイコールは見慣れているかと思いますが,実はこの等号は比に対しても使えます。例えば,一つ上の章で中身が同じである比として2:3と4:6を取り上げましたが,これは次のような等式に表せます。
2:3=4:6
このような等式は,実は「:」を使った比の形を外して整理できるのです。その方法は内側の数字と内側の数字,外側の数字と外側の数字をそれぞれかけ合わせるというものです。今回であれば内側というのは3と4,外側というのは2と6を指します。この2つのかけ算の積はどちらも12になるので辻褄が合いますよね。実際どんな比でもこの性質というのは成立するもので,この性質を使って一部が□で隠されている比の問題を解かされることが多々あります。内内外外という関係は忘れやすいですが,しっかりと暗記しておきましょう。

練習問題を解いてみよう
それでは軽く練習問題を解いて基礎編を終わりにしていきましょう。上の解説ページを振り返りながらでも構わないので,全問正解目指して頑張ってみてください。
(1)4:6と等しい比はどれですか。全て答えましょう。
8:6,12:18,1:1.5,0.2:0.3,32:42
(2)次の比を簡単にしましょう。
①3:2.7 ②1/2:1/4
(3)□に当てはまる数を答えましょう。
□:6=8:12
練習問題解説
それでは解説に移ります。中学受験で登場するレベルの問題ではありませんが,比と割合という範囲を振り返ったり導入したりするにあたっては,ちょうどいい水準の問題だったかと思います。もし間違えてしまったとしても次間違えなければいいだけの話なので,ゆっくり丸付けをしていきましょう。
まず(1)ですが,これは初めに4:6を簡単な比に置き換えた後に,選択肢として挙げられている比を一つずつ簡単にして一致するかどうか考えていけばいいですね。4:6は整理すると2:3になるので,選択肢を順番に見ていって2:3になるかどうか判断すればよいでしょう。ここで選択肢の日を計算してくと,8:6=4:3,12:18=2:3,1:1.5=2:3,0.2:0.3=2:3,32:42=16:21となるので,正解は以下の3つになります。
A.12:18,1:1.5,0.2:0.3
続いて比を簡単にする問題です。こちらは小数の比・分数の比ということでときづらかったかもしれせんが,基本原則は同じです。分数や小数の形を一度整数に戻し,そこから公約数で割っていくと答えに辿り着くことができます。まず0.3:2.7の比ですが,これは初めに10をかけて整数の比である3:27に直しましょう。そして3と27は両方とも3という数字で割り切れます。このことから答えは1:9となります。同様に1/2:1/4の方も,両辺に4をかけて整数の比である2:1に書き換えましょう。2:1という比はこれ以上簡単にできないので,答えは2:1になります。
A.(1)1:9,(2)2:1
最後は等号で結ばれた比の計算ですね。これは原則通り内と内・外と外をかけることで「:」を無くして計算を進めていきましょう。内と内のかけ算の結果は48,外と外のかけ算の結果は□×12となるので,次の式が成立します。
□×12=48
□=48÷12
□=4
このことから□の中身は4になります。手順さえ覚えれば意外とどの問題も簡単に解けるということをなんとなく理解していただければ幸いです。
A.4
追加練習用プリント(無料)
練習用プリント(無料)は、
『個別指導塾テスティー』の公式LINE の友だち追加された方のみの配布となっております。
以下から公式LINEの友だち追加をして、記事の続きをお楽しみください!!
≪入手方法≫
※画像はあくまでイメージです。本来送られるものとは違いますのでご了承いただけますよう、よろしくお願い致します。
①以下のリンクから公式LINEを友だち追加
②送信される画像をタップ!
パスワードで保護されている記事へと移動します。

③パスワードを入力(パスワードはLINEの友だち追加時に送信いたします。)
※パスワードを入力しても見ることができない場合、もう一度入力していただくか、キャッシュ機能の設定を変更するなどしていただきますよう、お願いいたします。

④スクロールしてPDFをダウンロード!

<スマートフォンからお読みの方はこちら>

<パソコンからお読みの方はこちら>
.png)
まとめ
今回は比の性質についてご紹介していきました。前述したように,比の性質というのは中学受験で必ずと言っていいほど登場しやすい単元の一つです。ぜひ早めのうちから対策をして,完璧にしておきたいところです。よろしければ下の記事や参考書籍を使いながら,更なる演習を重ねていきましょう。本記事が今後の勉強のお役に立てば幸いです。
おすすめ記事
参考
- 日能研教務部,「算数ベストチェック(チェックシリーズ)」(2000/9/15),みくに出版
- 小杉拓也,「改訂版 小学校6年間の算数が1冊でしっかりとわかる本」,かんき出版(2020)
- Z会指導部,「Z会中学受験シリーズ 入試算数の基礎30」,Z会(2010)

















