ここから本格的に運動の話に入る．まずは「運動を決定する」とはどういうことだったかを復習する．これについては力学の最初の記事でも述べているが，重要なことなのでもう一度触れる．その後，運動方程式から運動を決定する手順を見る．ここでは「時間追跡」というものについて説明する．聞いたことのない言葉かもしれないが，難しい概念ではないことがすぐに分かるはずである．
こうした言葉を使うのも，後に問題を解くパターンなどを理解する時に，「これは時間追跡で解く」というように端的に理解できると考えているからである．またそうした言葉を用いることで，説明を簡便にする目的もある．
この記事では一般的な話のみを扱う．具体的な問題はまた別の記事とする．そのため抽象的で難しいと思うかもしれないが，最初に力学の幹に当たる部分をおさえておくと，今後問題を解く際に，系統的に問題へアプローチができるだろう．
Contents
運動を決定するとは
まず「運動を決定する」とはどういうことだったかを思い出そう．それは「任意の時刻での物体の位置，および速度が分かっている状態」のことであった．そして加速度が分かれば，時間で積分することで速度や位置が得られることも見た．(忘れている場合は，力学の最初の記事で確認しよう．特に速度や位置を求めるための計算はすぐにできるようにしておこう．) だから物体の運動を決定するには，加速度を求める必要がある. そしてその加速度を決定する道具が運動方程式である．
運動方程式については，「力学の3 つの原理」の記事で述べたので，ここでは簡単な復習に留めておく．簡単のため1 次元を考えると，運動方程式は，
\(ma = F\) (1)と表せるのだった．左辺には物体の質量\(m\)と加速度\(a\)が含まれ，右辺には物体に働いている力\(F\)がある．この方程式の意味は，「質量\(m\)の物体にある力\(F\)が働くと，その物体は加速度\(a\)を得る」という意味になっている．右辺の力が原因となり，左辺の加速度が生じるという因果関係を表していることも既に説明した．
実は加速度の決定の説明はこれで尽きている．物体の加速度を決定するには，物体に働いている力を書き下し，運動方程式を用いればよい．言い換えると，運動の原因となる力が分かれば，結果としての加速度が分かるということである．そうして加速度が求まってしまえば，後は時間で積分して速度や位置を求めてしまえば良い．
いくつかの例を考えてみよう．以下の図1 のように，質量\(m\)の物体が力\(F\)を受けているとしよう．この記事では常にこの系を想定していると思ってほしい．この力としていくつかの仮定をして考える．
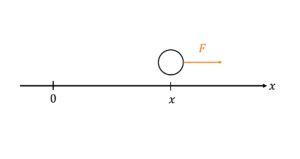図1: 力\(F\)を受けた物体．
時間追跡の簡単な例1
力\(F\)が常に一定の場合として，
\(F = k\) (\(k\) : 正の定数) (2)
であると仮定しよう．このとき運動方程式は，
\(ma = k\) (3)
である．これから簡単に加速度が決定できて，
\(a = \frac{k}{m}\) (4)である．速度と位置を決定するには時間で積分すれば良いから，
\(v(t) = \frac{k}{m}t+C\), \(x(t) = \frac{k}{2m}t^{2}+Ct+D\) (5)である．ただし\(C\), \(D\)は積分定数である．
これらの積分定数は初期条件で決まる．初期条件とは，物体が最初にあった状態，つまり最初の速度と位置の情報のことである．力学の「運動の記述」の記事を見返してもらえば分かるが，そこで扱っている例では，初期位置と初速度が与えられており，積分定数に相当する部分に，初速度や初期位置が入る．今回の例ではそのような初期条件を与えていないので，積分定数の部分は具体的に求まらない．
今見たように，運動法方程式から加速度を求め，物体の位置や速度を時間の関数で表すことができた．このように物体の運動，すなわち速度や位置を時間の関数で表すことを時間追跡という．
時間追跡の簡単な例2
もうひとつの例を見よう．今度は力が時間の関数になっていて，
\(F(t) = kt\) (\(k\) : 正の定数) (6)と表される場合を考えよう．先程と同様に運動方程式を立てると，
\(ma =kt\) (7)となる．これより加速度が
\(a = \frac{k}{m}t\) (8)と求まる．ここまでくれば後は時間で積分を繰り返すだけで，
\(v(t) = \frac{k}{2m}t^{2}+C\), \(x(t) = \frac{k}{6m}t^{3}+\frac{C}{2}t^{2}+D\) (9)と求まる．加速度から速度や位置を求める計算が慣れていれば，運動を決定するには運動方程式を書き下すだけで十分であることが分かるだろう．
以上の例から分かるように運動を決定するのは運動方程式である．運動方程式で加速度を決めれば，後は時間で積分するという計算のみである．ここまできて「よし，簡単だな」と思った人は待って欲しい．次の例を見てみよう．
時間追跡が簡単にできない例1
実は今まで見てきた例は，時間追跡が簡単になるような力を選んできていたのである．今度は時間追跡はできるが，簡単にはできない例を見よう．力として
\(F = -kx\) (\(k\) : 正の定数) (10)を考えよう．この力は既に見ている．弾性力である．ばねに繋がれた物体が受ける力である．この力が物体に働いている場合，運動方程式は，
\(ma = -kx\) (11)となる．ここで今までのように
\(a = -\frac{k}{m}x\) (12)とし，時間で積分して
\(v(t) = -\frac{k}{m}xt\) (13)とはしてはいけない．なぜならば，\(x\)はより正確に書けば\(x(t)\)であり，時間の関数だからである．しかも\(x(t)\)が時刻\(t\)を用いてどう表されるか分からない．というよりも今求めたいものが，\(x(t)\)である．
これではお手上げだと思うかもしれないが，そうではない．これも時間追跡ができるのである．まずは加速度が位置を時間で2 回微分することで表されることを思い出そう．すると運動方程式は，
\(\frac{d^{2}x\left( t\right) }{dt^{2}} = -\frac{k}{m}x(t) = -\omega^{2}x(t)\) (14)である．ここで便宜上，\(\omega^{2} = \frac{k}{m}\)と定義した．この式の意味は，ある関数を時間で2 回だけ微分したものが，自分自身のマイナス倍に比例するというものである．これは方程式の中でも，微分方程式と呼ばれるものである．「普通の」方程式と異なる点は，もちろん微分が含まれていることもそうだが，方程式を解いて求まるものが，「何かの値」ではなく「関数」が求まるという点である．
今回の例では，結果を述べてしまうと，方程式(14) を「解く」ことで，
\(x(t) = C\cos \left( \omega t\right) +D\sin \left( \omega t\right),\omega = \sqrt{\frac{k}{m}}\) (15)となることが分かる．この\(C\)や\(D\)は，今まで見てきた積分定数に相当するもの1である．実際にこの\(x(t)\)を方程式(14) の左辺に代入して，右辺になることを確かめてみよう．
ここで重要なことを述べる．方程式(14) のように，「ある関数を時間で2 回だけ微分したものが，自分自身のマイナス倍に比例する」微分方程式の解は，式(15) になることを覚えよう．もちろん導出をしても良いのだが，まずは解(15) が，微分方程式に代入して，確かに解であることを確かめれば良い．そしてこの解の形を覚えてくのが，受験的にも良いだろう．
速度は時間で1 回微分すれば求まる．今までと求まる順序が逆になっていることに注意しよう．この例の場合は，運動方程式から位置が分かり，速度が分かるという流れになっている．
時間追跡が簡単にできない例2
時間追跡はできるが，簡単ではない例をもうひとつ見ておこう．力として
\(F = -kv\) (\(k\) : 正の定数) (16)
を考えよう．これは空気抵抗などを表す時に，よく登場する．これも力に速度\(v(t)\)が含まており，速度の具体的な関数形が求めたいものそのものであるから，簡単に時間で積分とはいかない．
この例の場合は，加速度が速度を時間で1 回微分することで得られることを思い出すと，運動方程式は，
\(\frac{dv(t)}{dt} = -\frac{k}{m}v(t) = -\gamma v(t)\) (17)である． \(\gamma\)は表記上の便宜で導入した．今度は速度に関する微分方程式になっていることに注意しよう．前の例も今回の例も，右辺の力に含まれている関数を用いて，加速度を表すことがポイントになっている．
さてこの例も結果を覚えてしまおう．方程式(17) 解は
\(v(t) = C_{e}^{-\gamma t}\) (18)
である．方程式(17) のように，「ある関数を時間で1 回だけ微分したものが，自分自身に比例する」微分方程式の解は，式(18) になる．今回はマイナス倍はなくても成立する．これも方程式に代入して確かめてほしい．\(C\)は先程と同様に積分定数に相当するもの2である．
時間で積分して位置を求めることもできるが，受験の問題では速度がわかれば十分な場合が多いので，ここでは省略する．
時間追跡のパターン
時間追跡ができるものというのは，実は上で見たようなものに限られてしまう3．なのでまずは時間追跡ができるパターンを知り，それぞれどのように解を求めるかを身に付けておこう．時間追跡のパターンをまとめると，以下のようになる：
- \(F(t)\) = 定数，もしくは\(t\)の関数として具体形が分かっている時
→運動方程式から加速度を求め，時間の積分を繰り返す．
- \(F(t) = -kx\)の場合(時間の2 回微分が，自身のマイナス倍に比例する場合)
→\(x(t) = C\cos \left( \omega t\right) +D\sin \left( \omega t\right)\)を覚えておき，時間微分で速度を求める．
- \(F(t) = -kv\)の場合(時間の1 回微分が，自身に比例する場合)
→\(x(t) = C_{e}^{-\gamma t}\)を覚えておく．
- 上記に当てはまらない場合
→エネルギー保存則を考える．
時間追跡で計算できる場合は少ない．逆に言えば，時間追跡では解けない問題もある．そういう時はどうすれば良いかというと，エネルギー保存則である．これについてはまた次の記事で説明する．
1この微分方程式は正確には「2 階微分方程式」という．「回」ではなく「階」である．2 階微分方程式を解く作業は，積分を2 回行うこと等価で，積分定数に相当するものが2 個出てくる．
2この方程式は1 階微分方程式なので，1 つの積分定数しか出てこない．
3正確には他にもあるのだが，今は受験で主要なもののみを取り上げている．
おすすめ記事
参考
こんにちは。慶應義塾大学大学院物理学科の花井遼介です。
中学から大学生の前半くらいまではバドミントンをずっとやっていましたが、途中から勉強や研究が忙しくなり、最近ほとんどやっていません。なかなか運動をする機会が減って残念ですが、時々自転車の乗って知らない場所に行ったり、散歩をしたりしています。(特に研究に行き詰ったとき……)昔から理科が好きで、高校生の時に聞いた、とある物理学者の講演に感動して以来、大学では物理を専門に学びたいと思っていました。現在は原子核理論の研究室に所属しています。その中でも僕は中性子星という超高密度な天体を、原子核理論の立場から研究しています。物理が好きでそれを専ら学んでいることもあって、高校生向けに高校物理や大学に入ってからの物理、物理学科についてなどの記事を提供していこうと思います。高校物理の記事でも、僕が大学に入って得た知識や理解をもとに、受験に役立つのみならず、学問としての面白さが含まれるような記事を書くつもりです。(受験向けの部分とそうでない部分は分かるように書くつもりですので、興味や必要に応じて読んでもらえればと思いま。)
僕の書く記事は、あくまで読者の皆さんの「補助的なもの」です。最終的には自分で勉強する、ということが大事になります。なので記事をきっかけに、皆さんが自分で物理を勉強できる状態になれれば、僕の目標は達成されたことになります。
僕の記事からさらに自分でもさらに深く勉強してほしいと思います。
皆さんと共に物理の面白さに触れ、理解を深められることを願っています。
