今回の記事では速さと比の計算の解き方の導入として,「そもそも速さってなんだっけ?」ということを中心にお教えしていきます。速さというのは小学生の中学年ごろから習い始める単元ですが,計算の複雑さから苦手に感じる人が多い範囲です。しっかりと対策しておくことが必要不可欠なので,是非一読ください。
Contents
速さと比の計算とは?
そもそも速さと比の計算とはどのような文章題を指すのでしょうか。試しに例題を見てみましょう。次の3つのような問題が,入試に登場する速さと比と呼ばれる問題の一例です。
学校から公園まで行くのに,Aくんは10分,Bくんは20分かかります。AくんとBくんの速さの比を求めなさい。
学校から公園まで行くのに,Aくんは分速30mで,Bくんは分速50mで歩きます。Aくんが出発してから到着するまで25分かかるとき,Bくんのかかる時間は何分になるでしょう。
Aくんが学校と公園を往復するのに,行きは分速80mで,帰りは分速60mで歩きました。往復でかかった時間が2時間20分のとき,学校と公園までの距離は何kmになるでしょう。
この3つを並べてみると分かるかもしれませんが,このように道のり・時間・速さが関係する問題のことを速さと比の計算と言います。ただしそれだけが重要なのではありません。速さと比の問題において重要なことが,道のり・時間・速さのうちある1つの要素が全く同じ値になっていて,それ以外の要素については2種類の数値が与えられるということです。例えば今回の問題ですと,1問目はAくんとBくんの2人が登場していて,2人とも学校から公園までを歩くため,道のりの大きさが等しくなっていますね。そのため,それぞれの道のり・時間・速さの3要素をまとめると,下の図のように整理できるわけです。
このように,ある要素を基準として中身を整理し,まとめた内容に基づいて他の要素の大きさを比べていくという作業が速さと比の計算では必要になってきます。今回の記事で速さと比の問題を解く上での前提となる速さの考え方や,比の計算方法などについてお教えしていくので,攻略法の紹介はこの辺りにとどめておきます。気になった方がいれば,次の【発展編】や【応用編】の記事でご確認していただけますと幸いです。
「道のり・時間・速さ」の意味!
ここまでの説明を聞き,「そもそも道のり・時間・速さとは何だろう?」と思った人も少なくはないでしょう。速さに関する要素は低学年中学年だけでなく,受験を意識し始める高学年のお子様でも,きちんと理解できている人は意外と少ないのではないでしょうか。そこで基礎編の本記事では,時間に関する用語をまとめることから始めていきます。
まずは全ての基準となる道のりから順番に説明していきます。道のりとは,問題によっては距離と言われることもある,人やバス・自転車などの動いているモノが出発した地点から到着した地点までの長さのことを指します。
次に時間ですが,これは動いているモノが出発した時刻から到着した時刻の間隔のことを意味します。慣れないうちは時計が示す1時間という単位と混合してしまうかもしれませんが,あくまで間隔という意味なので,問題によって単位は秒・分・時間・日など異なります。特に速さを習いたての人は気をつけて覚えておきたいところです。
最後に速さですが,こちらは上でご紹介した道のりと時間から定義されるものです。速さとは,動いているモノが一定の時間あたりに進んだ距離のことを言います。このときの一定時間というのは時間と同様問題によって異なるのですが,1秒あたり・1分あたり・1時間あたりとなることがほとんどで,それぞれの単位における進んだ距離を秒速・分速・時速と表します。例えば秒速30mという数値があれば,それは1秒という単位時間あたりに30m進むということと同じ意味になります。速さ・スピードといった単語は日常生活でも使われますが,算数の中で使われると意外に困ってしまいがちです。しっかり理解しておきましょう。
これらの定義は一見受験やテストを攻略する上では不要に見えますが,問題が難しくなるほど必要になってきます。長い文章題や複雑な設定の問題だと線分図を使いながら問題を整理しなければならなくなるのですが,そのようなときに用語の意味がきちんと把握できていないと,間違った認識のもと間違った解答が導かれてしまいます。もちろん公式を覚えておくことも大切ですが,それと同じくらい基礎的な用語の意味にも注意しながら理解を深めていきましょう。
公式を覚えよう!
ここからは公式の説明に移ります。先ほどの説明の中で,速さとは動いているモノが一定時間に進んだ距離のことを指すと申し上げました。そのためモノが進んだ道のりを秒/分/時間といった時間で割っていけば,そのモノが1秒/1分/1時間あたりに進んだ量,つまり速さを計算することができます。これを式にまとめると下のようになりますね。
①速さ=道のり÷時間
また速さに関係する式はこれだけではありません。この①の式の「÷時間」に注目してみましょう。この時間の部分を両辺にかけると,次のような式を得ることができます。
②道のり=速さ×時間
このように速さを求める式も道のりを求める式も存在するのですが,加えて時間を求めるための計算式も覚えておきましょう。②の式の「速さ×」の部分に注目してみます。いまこの式の両辺を速さで割ってみると,次のような式が生まれ,道のりと速さの値から時間を求められるようになります。
③時間=道のり÷速さ
この3つの公式を覚えるのは,慣れないうちは難しく感じるかもしれません。テキストや参考書の問題を解くくらいなら公式を見ながら解くことができますが,テストや受験本番ではそうはいきません。もちろん問題を解きながら覚えることもできますが,今回は速さに関する関係をできるだけ早く覚えるための2つの考え方をご紹介します。これらに考え方は暗記が必要なものではないですし,どちらか片方のイメージで理解しておけば十分ですので,あまり気負わずに頭に入れておきましょう。
考え方① 面積の求め方で覚える
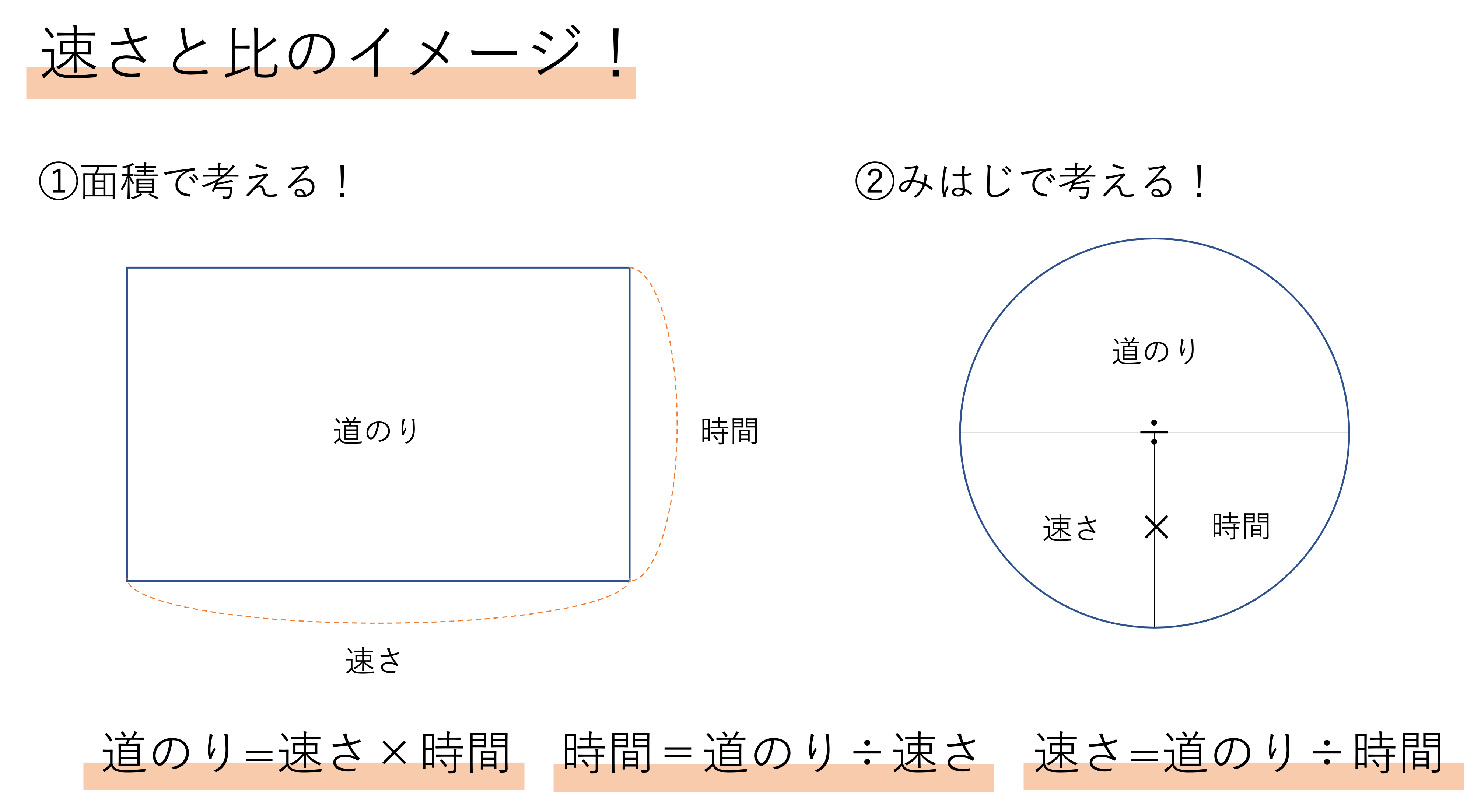
1つ目の覚え方は四角形の面積の求め方をイメージすることです。面積をあえて使うのは,低学年のお子様でも慣れ親しみがあるからです。四角形の面積はたて×よこ=面積という公式で求めることができました。今回はこの公式になぞらえて速さの考え方を覚えていくことがポイントです。
たて×よこ=面積,という式は道のり=速さ×時間という式と似ていますね。そのため面積を道のりに,たてを速さに,よこを時間に見立てて理解することで,3つの公式を一気に覚えることができます。この面積のイメージを覚えていると,もし道のり=面積が求めたかったら速さ=たてと時間=よこをかけ算すればいいですし,もし速さ=たてが求めたかったら道のり=面積を時間=よこで割ればいいですし,もし時間=よこが求めたかったら道のり=面積を速さ=たてで割ればいい,ということが一発でわかるようになります。
ただ難点としては,四角形の面積に関する理解が中途半端だと,かえって面積の単元も速さの単元も分かりづらくなってしまうことが挙げられるでしょう。そのような場合は下でご紹介する「みはじ」の図を使ってみてください。
考え方② 「みはじ」の図で覚える
2つ目の覚え方は「みはじ」の図をイメージすることです。この図は,道のりの部分が距離になって「みはじ」と言われることもありますが,同じものを示すと思っていただければ幸いです。学校や塾などで聞く覚え方は主にこのパターン②の方なので,読者の皆様の中には見たことある人もいるかもしれませんね。この図は円を3つのパーツに分け,その中に「み」=道のり,「は」=速さ,「じ」=時間を当てはめることで計算式を覚えていくというモノです。
この「みはじ」の図の書き方ですが,まず円を書き,その後に半円とおうぎ形2つに分けて半円の部分に道のりを,残ったおうぎ形に速さと時間を記入していきます。そして図の中の横に伸びる直径を「÷」・下に伸びる半径を「×」だとみなすと,正しい計算方法を知ることができるのです。例えば道のりが求めたければ残った速さと時間をその間の×でつなげばいいですし,速さが求めたければ残った道のりと時間をその間の÷でつなげばいいですし,速さが求めたければ残った道のりと時間をその間の÷でつなげばいいですね。
しかしこの図にも弱点があり,それは図を正確に書けなければ全ての計算が間違ってしまうということです。それぞれの要素や記号の位置がなかなか覚えられそうになかったら,上でご紹介した面積のイメージを使って頭に入れていただけますと幸いです。
終わりに
今回の問題では速さと比という文章題に関して,その基本となる速さの定義を中心に解説していく記事でした。前述したように,基本的な用語の意味や公式が分かっていないと実際に入試で登場したときに対処しにくいです。この速さと比という単元は受験生がつまずきやすいので,よろしければ下の参考書籍やおすすめ記事を使いながら,更なる学力向上を目指して頑張ってみてください。


















