1.式と証明～恒等式、未定係数法、等式の証明、絶対不等式をマスターしよう〜[数学2]| 中学受験ナビ

Contents

1 恒等式
2 不等式
3 おすすめ記事
4 参考

恒等式

恒等式・・・\(\forall x\{x|f(x)=g(x)\}\)
分数式が恒等式⇒分母を払った整式も恒等式（分数式や整式を有理式という）
部分分数分解
- ①\(\frac{1}{n(n+1)}=\frac{1}{n-1}-\frac{1}{n+1}\)
- ②\(\frac{1}{(2x-1)(x+1)}=\frac{a}{2x-1}-\frac{b}{x+1}\)が恒等式の時の値\(\begin{pmatrix} a \\ b \end{pmatrix}\)を求めよ。
  - <共通方針>
    与式が恒等式⇒分母を払っても恒等式
    \(1=a(x+1)+b(2x-1)\)
  - 〈解法1〉
    \((a+2b)x+a-b-1=0\)より
    \(\begin{cases}a+2b=0\\ a-b-1=0\end{cases}\)⇔\(\begin{pmatrix} a \\ b \end{pmatrix}\)=\(\begin{pmatrix} \frac{2}{3} \\ -\frac{1}{3} \end{pmatrix}\)
  - 〈解法2〉
    \(x=-1\)を代入
    \(1=-3b\)より\(b=-\frac{1}{3}\)\(x=\frac{1}{2}\)を代入
    \(1=\frac{3}{2}a\)より
    \(a=\frac{2}{3}\)なので
    \(\begin{pmatrix} a \\ b \end{pmatrix}\)=\(\begin{pmatrix} \frac{2}{3} \\ -\frac{1}{3} \end{pmatrix}\)

未定係数法…\(\forall x\{x|f(x)g(x)\}\land f(x)=\sum ^{n}_{i=0}a_{i}x^{i}\forall g(x)=\sum ^{n}_{i=0}b_{i}x^{i}\)

係数比較
\( ai=bi　or　ai-bi=0\)を示せばよい
\(\forall x\lbrace x\mid ax^{2}+bx+c=ax^{2}+a(\alpha +\beta )x+a\alpha \beta =0\rbrace \)
⇔ \(\begin{cases}b=-a(\alpha +\beta )※\\ c=a\alpha \beta \end{cases}\)※は解と係数の関係
or　\(∀x\lbrace x|\lbrace b+a(\alpha +\beta )\rbrace x+c-a\alpha \beta =0\rbrace
\)とも書ける
\(b+a(\alpha +\beta )=0, c-a\alpha \beta =0\)
代入法　
n次式なら係数はn+1個　→ n+1個の値を代入
Ex. 整式は\(-5f(x)=f(x-1)+2f(x+2)=29\)の恒等式を満たす。
1. \(f(1)f(0), f(1), f(-1)\)の値を求めよ。
  \(x^{2},x,\)定数それぞれの係数を\(a,b,c\)とおくと、
  1. \(x=0\)を代入
    \(-5f(0)=f(-1)+2f(1)=29\)となり、
    \(5a+2b+c=29\)
  2. \(x=1\)を代入
    \(f(0)-5f(1)=2f(0)-33\)となり、
    \(a+5b=33\)
  3. \(x=-1\)を代入
    \(-f(0)-5f(-1)=4f(0)-25\)となり、
    \(a+c=5\).
    以上より
    \(5a+2b+c=29\),
    \(a+5b=33\),
    \(a+c=5\).
    したがって\( \begin{pmatrix} a\\b\\c\end{pmatrix}=\begin{pmatrix} 3\\6\\2\end{pmatrix}\).
2. \(f(x)\)の次数を求めよ。
  1. \(f(x)\)を定数とする。
    (左辺)=1次式、(右辺)=3次式より不適
  2. \(f(x)\)をn次式(n>1)とする。
    (左辺)=2n+1次式、(右辺)=n+3次式より
    \(2n+1=n+3\) より \(n=2\).
3. \(f(x)\)を求めよ。
  \(f(x)\)は2次式であるから、\(f(x)=ax^{2}+bx+c( a\neq 0)\)とおける。
  また、\(f(0)=3よりc=3\).
  \(f\left( x\right) =ax^{2}+bx+ 3\)であるから
  \(f(1)=a+b+3=6\)\(f(-1)=a-b+3=2\)より
  \(\begin{pmatrix} a \\ b \end{pmatrix}=\begin{pmatrix} 1 \\ 2 \end{pmatrix}\)である
  \(f(x)=x^{2}+2x+3\)

等式の証明

恒等式であることを示す。

A=Bを示すのに、

〈解法1〉A-B=…=0 オススメ‼︎
〈解法2〉B 0,A/B=…=1
〈解法3〉A=C B=C ⇒ A=B …三段論法
〈解法4〉A=…=B (易問のみに使用)

のいずれかを用いる。

条件として与えられることが多いのが、以下の2つ。

等式⇒代入して文字を消去
比⇒パラメーターで代入

不等式

評価

評価とは不等式を作ることを指す。以下によく使うテクニックをまとめる。

差>0、比>1
- 平方完成
- -1<sinθ<1
図形(線分・面積)
- 積分
絶対不等式
- 相加相乗平均
- コーシーシュワルツの不等式
- 三角不等式
グラフ
- 増減
- 凸性
- 積分
実数の存在条件
- 2次方程式の判別式
- グラフの交点
- 中間値の定理

絶対不等式

①相加相乗平均; 使いどころは逆数
\(a >0,b >0\Rightarrow \frac{a+b}{2}\geq \sqrt{ab}\)で、等号条件は\(a=b\)のとき
証明)
- (i)差
  左辺-右辺=\(\frac{a+b}{2}- \sqrt{ab}\),
  \(=\frac{1}{2}(a- 2\sqrt{ab}+b)\)
  \(=\frac{1}{2}(\sqrt{a}-\sqrt{b})^{2}\)>0
- (ii)図形
  \(a:h=h:b\),
  \(h^{2}=ab\),
  \(h=ab\)以上より\(1+\frac{b}{2} >ab\)

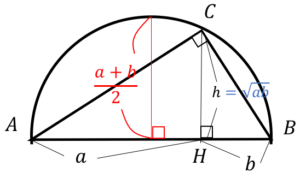
図1　相加相乗平均　証明（図形）　　AHC∽CHBより

- (iii)グラフ
  グラフの凸性より
  \(\log_{10} \frac{a+b}{2}>log_{10}a+log_{10}\frac{b}{2}\),
  \(log_{10} \frac{a+b}{2}>ab\).
  \(log_{10} x\)は単調増加であるから
  \(\frac{a+b}{2}>ab\)

図2　相加相乗平均　証明（グラフ）

②コーシー・シュワルツの不等式; 使い所は平方
2乗≧積の2乗
- 2次元\((x,y), (a,b)なら(x^{2}+y^{2})(a^{2}+b^{2})>(ax+by)^{2}\)
- 3次元なら\((x,y,z), (a,b,c)なら(x^{2}+y^{2}+z^{2})(a^{2}+b^{2}+c^{2})>(ax+by+cz)^{2}\)
- \(a^{2}+b^{2}>(ab)^{2}\)
- 証明)
  - \(S=\frac{1}{2}ab sinθ\),
    \(=\frac{1}{2}a^{2}b^{2}sinθsin^{2}θ=1-cos^{2}θ\),
    \(=\frac{1}{2}\)根号の中身は正なので、\(a^{2}b^{2}\)>( abcosθ)²
  - 内積
    \(OA=a=p^{2}+q^{2}\),
    \(OB=b=r^{2}+s^{2}\)より\((p^{2}+q^{2})(r^{2}+s^{2})>(pq+rs)\)

図3　コーシー・シュワルツの不等式　証明

問題演習

①不等式\(x^{2}+y^{2}+z^{2}>xy+yz+zx\)を証明せよ。また等号の成立条件を求めよ。
- 〈解法〉
  平方を作って評価する。
  左辺-右辺=\( x^{2}+y^{2}+z^{2}-xy-yz-zx \),
  \(=(x-y)^{2}+xy+(y-z)^{2}+yz+(z-x)^{2}+zx-(x^{2}+y^{2}+z^{2})\),
  \(=(x-y)^{2}+(y-z)^{2}+(z-x)^{2}-(x^{2}+y^{2}+z^{2}-xy-yz-zx)\),
  \(=\frac{1}{2}\lbrace(x-y)^{2}+(y-z)^{2}+(z-x)^{2}\rbrace>0\)より成立。
  また、等号が成立するのは、\(x=y=z\)の時。

※以下知っておくと便利な公式

\(a^{2}+b^{2}+c^{2}-ab-bc-ca=\frac{1}{2}\lbrace (a-b)^{2}+(b-c)^{2}+(c-a)^{2}\rbrace\)
\((a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2(ab+bc+ca)\)
\(a^{3}+b^{3}+c^{3}-3abc=(a+b+c)(a^{2}+b^{2}+c^{2}-ab-bc-ca)\).

②実数xについて、\(A=x^{4}+5x^{3}+5x^{2}+2x+7\)、\(B=x^{2}+2x+2\)とおく時、AとBを用いて表せ。また、A/Bの最小値とその時のxの値を求めよ。
- 〈解法〉
  Bを変形して\(x^{4}\)を作る。
  \(B^{2}=x^{4}+4x^{3}+4x^{2}+8x+4\)より
  \(A=B^{2}-3B+9\)となり、
  \(\frac{A}{B}=B-3+\frac{9}{B}\),
  このとき\(B>0より9/B>0\)\(B+\frac{9}{B}\)の最小値は相加相乗平均より、
  \(B+\frac{9}{B}>6\),
  ∴\(B-3+\frac{9}{B}>3\),
  また、\(B-3+\frac{9}{B}=3⇒B=3\),
  \(x^{2}+2x+2=3\)より
  \(x=-1±2i\)