今回の記事では,水の深さと体積という範囲について取り扱うシリーズの第2段目として,モノの水没に関する問題の攻略法をご紹介していきます。この問題は場合分けが必要となり,初めて見ただけではなかなか答えまで辿り着けないことが多いです。そのため早い段階から対策しておくことが肝心です。よろしければ本記事を一読していただき,得点力アップにつなげていきましょう。
「モノの水没」とは?
それではここから解説の本編を始めていきます。まずはモノの水没がどういった問題を指すのか,といった事項をお教えしていきます。この問題では石をはじめとした何らかの物体を水の入った容器の中に沈め,水のかさがどのくらい増えたかが問われます。読者の皆様もお風呂に入ったときちょっと水位が上がったり水が溢れたりした経験があるかと思われますが,この現象を算数の観点から捉えたのがこの「モノの水没」問題になるわけです。例えば中学受験では次のような問題が出題されます。文章の特徴などを掴んでおきましょう。
たて20cm,よこ20cm,高さ15cmの水槽に,深さ10cmのところまで水が入っています。この水槽の中に石を沈めたところ,水面は12cmまで上がりました。石の体積は何cm3でしょう。
底面積が100cm2の容器の中に,10cmの深さまで水が入っています。ここに底面積が20cm2で高さが15cmの棒を,底に対して垂直になるように沈めていきます。棒を1本入れたとき,水面の高さは何cmになりますか。
このように水槽に何かを沈める・入れるという操作が行われていたら,それは水没の問題だと判断して計算を進めてしまっていいでしょう。今回はこれらの問題を基にして,攻略法をご紹介していきます。
モノの水没問題の攻略のポイント!
ここからは水没の基本の問題をどうやって解けばいいか,についてご紹介していきます。まずこれらの問題を解く上で重要なポイントが,入れた物体の堆積と増えたかさの量は同じであるということです。石でも棒でも人の身体でもそうですが,水の中に物体を入れたとき,その水は押し上げられるために水面が上昇し,元々の量より増えたように見えます。しかし中に入っている水の量に変化が生じたわけではないので,ここで増えたように見える水の量は入った物体の体積と等しいと言えるわけです。この前提を活かしながら,先ほどご紹介した問題を解き,解答の一連の流れを抑えておきましょう。
たて10cm,よこ20cm,高さ15cmの水槽に,深さ8cmのところまで水が入っています。この水槽の中に石を沈めたところ,水面は12cmまで上がりました。石の体積は何cm3でしょう。
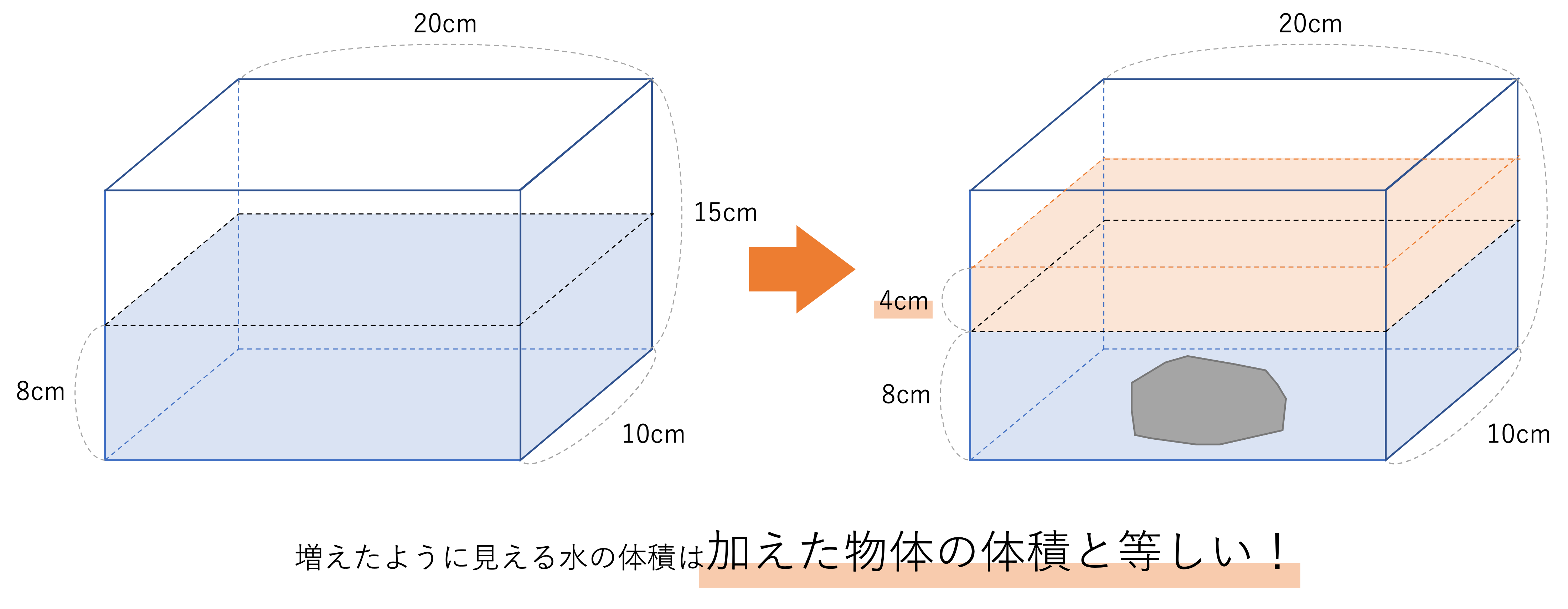
この問題を増えたように見える水の量=物体の体積という関係から読みといていきます。今回の問題では石を加えたところ水面が4cm上昇したという指示が与えられていましたが,この上昇分が石の体積と等しいと考えると,増えたように見える水の量が何cm3であるかを計算すれば答えが求められそうですね。
そして前回の記事でも確認しましたが,モノの体積や容積を計算するには底面積×高さを計算すればいいですね。今回増えた水の量の底面積は水槽の底面積と等しく,高さは上昇分の4cmとみなすことができるので,答えは10×20×4=800cm3となります。
A.800cm3
ちなみにこのようなモノを水没させるというちょっと馬鹿げているようにも思える行動ですが,実際に理科や科学の実験などで使用される手法でもあります。上で登場させた石などはゴツゴツしているため底面積×高さで体積を計算できそうにありません。そこで代わりに水の中に物体を沈め,かさがどれくらい増えたかで体積を求めることがあります。テストに出ることはないでしょうが,参考までに覚えておきましょう。
全水没と半水没に気をつけよう!
ここからは少しレベルの高いモノの水没問題の解説に移ります。先程の問題では増えた水の体積は加えた物体の堆積と等しい,という説明を行いました。しかし中学受験に登場する問題の中にはよりレベルの高いものがあります,それが半水没の問題です。先ほどの石を沈める問題では全体を沈めるという全水没の場合が想定されていましたが,それに対し物体の一部が沈んで一部は水に浸かっていない半水没の問題は簡単に増えた水の体積が計算できないため,解きにくい問題になってしまいます。というのも半水没の場合,増えた水の底面積が水槽の底面積と一緒にならないからです。違いを分かりやすく説明すると,次の図のようになります。
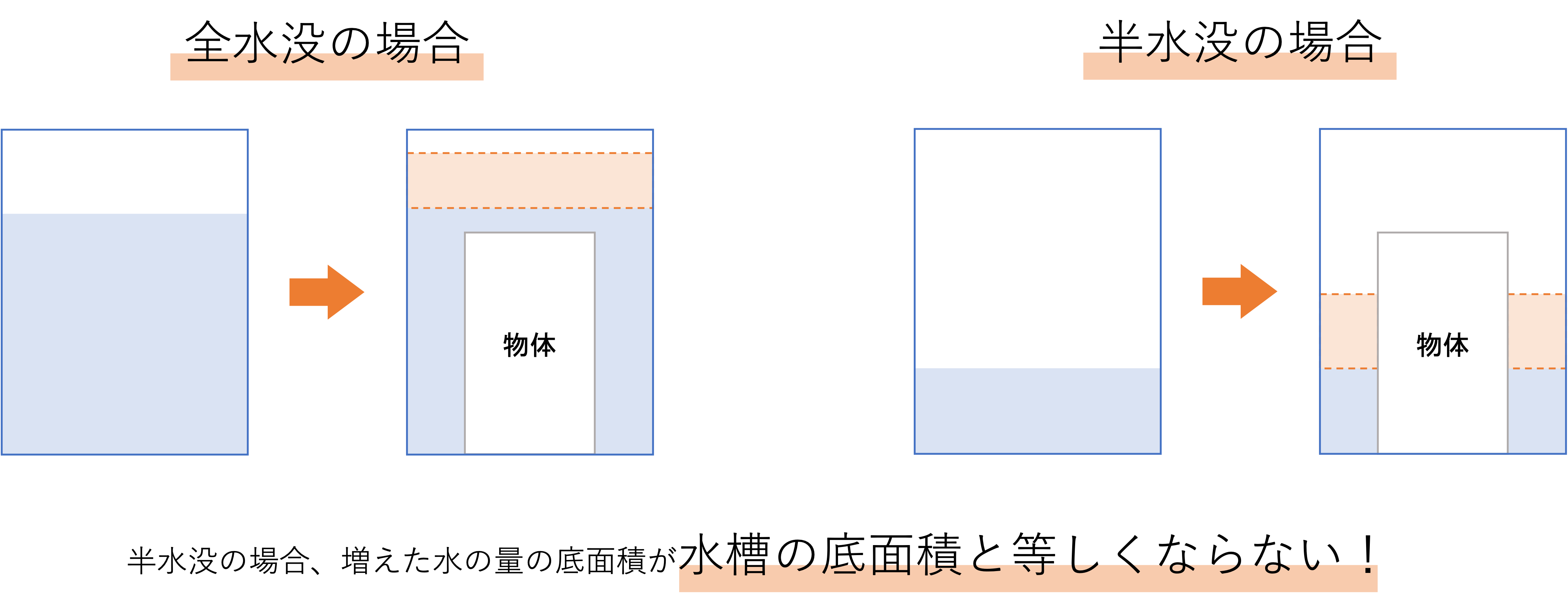
先ほどご紹介した問題の後者も,この半水没の問題に当てはまります。改めて引用してみましょう。
底面積が100cm2の容器の中に,10cmの深さまで水が入っています。ここに底面積が20cm2で高さが15cmの棒を,付加に対して垂直になるように沈めていきます。棒を1本入れたとき,水面の高さは何cmになりますか。
このような問題が登場した場合に,先ほどの全水没と同じ要領で解いてしまうと間違った答えが導かれてしまうというわけです。この半水没の問題でも重要なのは,中に入っている水の量は変化しないということです。以上の点に注目し。この問題を使いながら半水没の問題の攻略法をご紹介していきます。解き方のステップですが,まずは物体を入れる前の水の量を計算していきます。今回の問題では容器の底面積が100cm2であり,その容器の10cmの高さまで水が入っていますね。そのため水の体積は100×10=1000 cm3になります。
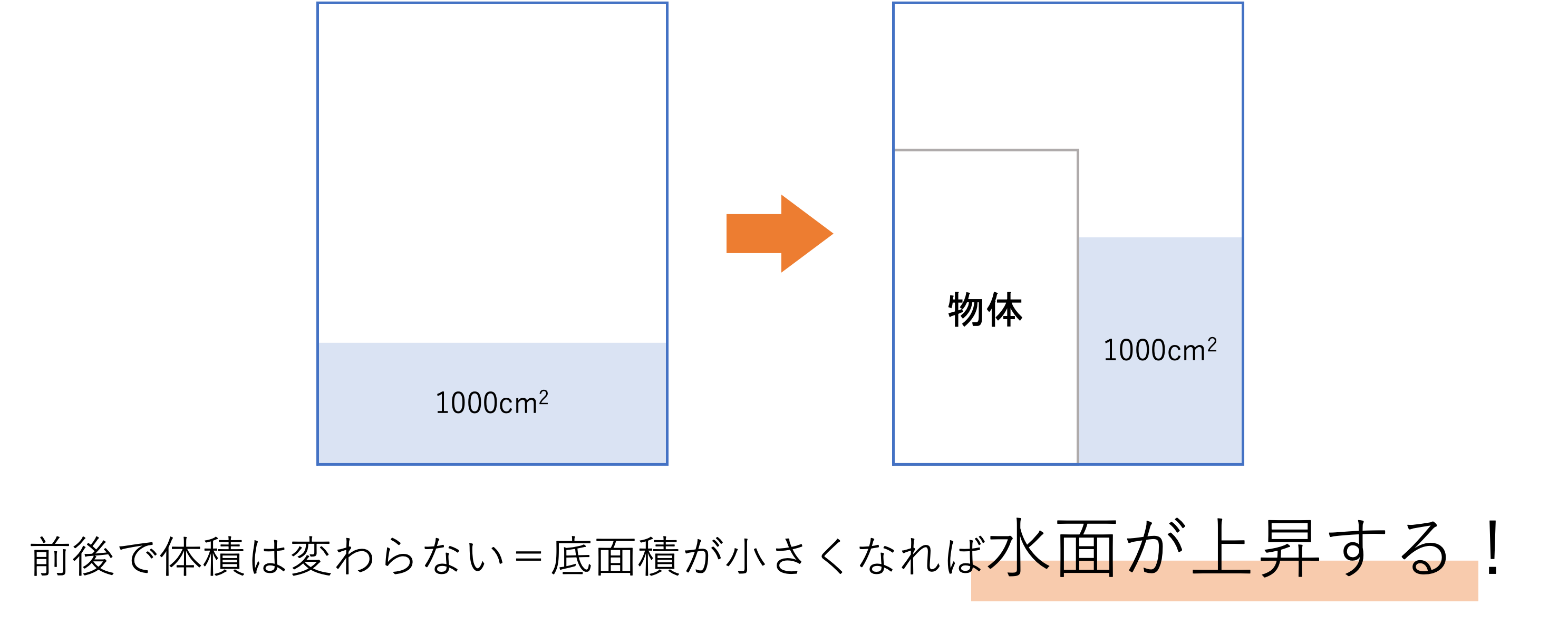
さて,ここからが半水没特有の操作になります。先ほども申し上げた通り,半水没の問題では物体を入れることで水の入っている部分の底面積が変化します。しかし体積が一定のままなので,その状態で底面積が小さくなると,反比例の関係から高さが増えていくのです。これらのことから,物体を入れた後の容器の底面積で元々入っていた水の量を割ってあげることで,水の高さがどれくらいになっているかを計算することができます。今回は物体の底面積が20cm2であることから,容器の底面積は80cm3と変化します。この値をもとにして水面の高さを計算すると,
1000cm3÷80cm2=12.5cm
となるため,答えは12.5cmとなります。このようにして①元々の水の量を計算する→②物体を入れた後の底面積で割る,という操作を辿れば無事答えを導くことができます。
A.12.5cm
全水没か半水没かを見極めるポイントは…?
ただしここで注意しておきたいところが,まだこの時点では半水没か全水没かが確定していないということです。全水没と半水没の違いは,水面よりも物体の高さの方が高い位置かどうか,という状況の差にありました。そのため今解いている問題が全水没か半水没かを求めなければ計算に進むこともできません。したがって問題を解く前の段階でどちらに該当しているかを判断しなければならないのです。
見極めるポイントの1つ目が,問題文で水に入れる物体の高さが設定されているかどうかです。物体の高さが示されていない問題は,その情報を使う必要がないから省かれているといみなすことができ,それゆえに高さが与えられている問題は全水没・与えられていない問題は半水没であるケースが多いです。
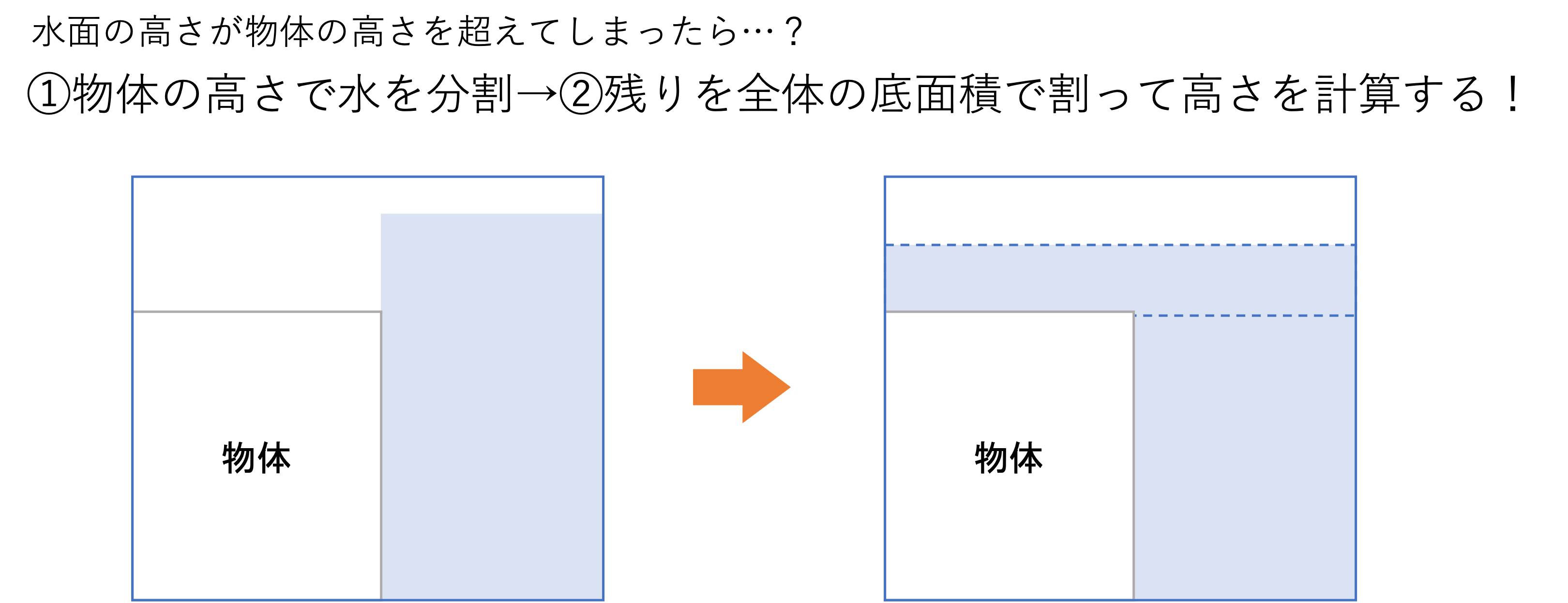
ただし,中にはひっかけの問題も存在します。そのため2つ目のポイントとして,底面積で割ったときの値が物体の高さを超えるかどうかで判断するとよりよいでしょう。例えば先ほどの問題では物体の高さが15cmでしたが,水面の高さが12.5cmにしかならないので半水没の問題だと断定できます。他方水面の高さが物体の高さを超えてしまった場合は,その高さまでの分で一度水の量を分割し,残りを全水没の要領で割り算して計算していくと正しい答えを計算できます。特に難関校の入試ではこのような引っ掛け問題が登場しやすいので,気を付けておきましょう。
おわりに
『個別指導塾テスティー』の公式LINEにて、
『中学受験を9割成功に導く』メールマガジンを
毎週、完全無料で配信中✨
塾の活用の仕方・最適な勉強法・親として子供をどう教導するかの指針など 中学受験するお子様を持つ親御さんが知りたい知識を幅広くご紹介!!
↓↓詳細は以下をタップ↓↓



















