10.反応速度と化学平衡②〜化学平衡の関係を利用できるようになろう〜[大学受験化学-理論化学]

弱酸の電離平衡

3章で見たように強酸は定義から電離度α=1なので、HCl→H⁺ + Cl^– のように100%完全に電離している。
一方で弱酸はα≪1なので、一部は電離するが、電離していないものも存在する。
これはいわゆる正反応も逆反応も混在している状態であり、電離平衡状態にあるとみなせる。
たとえば酢酸は、CH₃COOH ⇄ CH₃COO^– + H⁺ の様に表記できる。

この平衡定数を考えると、

\(\frac{[CH_{3}COO^{-}][H^{+}]}{[CH_{3}COOH]}=(一定)=K_{a}\)

となり、この\(K_{a}\)を酸の電離定数(解離定数)をいい、温度が一定なら決まった値になる。

そこでこの\(K_{a}\)と電離度α、酢酸の濃度Cの関係を見ていく。

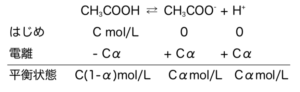
式1

これを平衡定数に代入し、

\(K_{a}=\frac{Cα・Cα}{Cα}=\frac{Cα^{2}}{1-α}\)

いま、酢酸は弱酸なので、α≪1より、1-α≒1とみなせる。

よって\(K_{a}=Cα^{2}\)となり、

\(α=\sqrt{\frac{K_{a}}{C}}\)

と求まる。また、

\([H^{+}]=Cα=C・\sqrt{\frac{K_{a}}{C}}=\sqrt{CK_{a}}\)

である、ここからpHを考えていける。

これらの導入はいつでも自力で出来るようにしてほしいが、一応公式としてまとめておくと

〈弱酸の電離平衡(オストワルトの希釈律)〉

\(α=\sqrt{\frac{K_{a}}{C}}、[H^{+}]=\sqrt{CK_{a}}\)

• Ex)酢酸の電離定数\(K_{a}=4.0\times10^{-5}mol/L\)をとすると、0.1mol/Lの酢酸水溶液の電離度はいくらか？

\(α=\sqrt{\frac{K_{a}}{C}}\)

より、

\(α=\sqrt{\frac{4.0\times10^{-5}}{0.10}=2.0\times10^{-2}}\)

※このオストワルト希釈律は酢酸のように1-α≒1と見なせるときにしか使えない。
目安としては、αが１より2ケタ以上小さければ近似してよい。
たとえば、先ほどの例ならα=2.0×10^-2ということで2ケタ違うのでOK。
これが、計算して2ケタ未満の差だった場合は、\(K_{a}=\frac{Cα^{2}}{1-α}\)よりαに関する二次方程式を解いてαを求めるしかない。

なお、H₂Sのような2価の弱酸の二段階の電離を考えないといけない。
〈1段階目〉H₂S ⇄ HS^– + H⁺

\(K_{1}=\frac{[HS^{-}][H^{+}]}{[H_{2}S]}\)

〈2段階目〉HS^– ⇄ S^2- + H⁺

\(K_{2}=\frac{[S^{2-}][H^{+}]}{[HS^{-}]}\)

一般に2価の酸では\(K_{1}\)に比べて\(K_{2}\)は非常に小さく、2段階目の電離はほぼ無視できるくらいにしか起こらない。

なお、\(K_{1} \times K_{2}\)によって全体の平衡定数も表せ、

\(K_{1} \times K_{2}=\frac{[HS^{-}][H^{+}]}{[H_{2}S]} \times \frac{[S^{2-}][H^{+}]}{[HS^{-}]}\)

となる。

弱塩基の電離平衡

アンモニアの電離平衡 NH₃ + H₂O ⇄ NH₄⁺ + OH^– を考える。
これも同様に平衡定数を考えると、\(\frac{[NH_{4}^{+}][OH^{-}]}{[NH_{3}][H_{2}O]}\)となりそうなものだが、平衡定数において一般に溶媒のH₂Oは多量にあるため、何を溶かしてもH₂Oのモル濃度は一定をみなせ、これも平衡定数に組み込んでしまうことになっている。

よって、

\(\frac{[NH_{4}^{+}][OH^{-}]}{[NH_{3}]}=(一定)=K_{b}\)

※bはbaseより。

となり、\(K_{b}\)を塩基の電離定数をいう。

また、塩基についても同様に1-α≒1とみなせる場合はオストワルトの希釈律が成り立ち、

\(α=\sqrt{\frac{K_{b}}{C}}、[H^{+}]=\sqrt{CK_{b}}\)

の関係がある。

水のイオン積

水H₂Oもわずかに電離しており、H₂O ⇄ H⁺ + OH^– の電離平衡が成り立っている。

これも同様に平衡定数を考えると、\(\frac{[H^{+}][OH^{-}]}{[H_{2}O]}\)となりそうであるが、”弱塩基の電離平衡”と同様で多量にあるH₂Oのモル濃度は一定とみなし、定数に組み込むことで

\([H^{+}][OH^{-}]=(一定)=K_{w}\)

※wはwaterより。

という式が導かれ、この\(K_{w}\)を水のイオン積という。
この\(K_{x}\)は25℃では1.0×10^-14mol²/L²であることがよく知られており、平衡定数なので温度が変われば値も変わる。

実際、H₂O ⇄ H⁺ + OH^– -56.5kJ という吸熱反応であるため、ルシャトリエの原理から温度を上げると平衡は右にすすむ。

よって水のイオン積は高温にするほど大きくなる。

pHと水素イオン濃度　~復習~

pHと水素イオン濃度の定義

水溶液の酸性・塩基性の強さを表す数字をpHという。
pHは0~14の範囲で、7を中性とし、7より小さいと酸性、7より大きいと塩基性を表す。

図1

このpHは水溶液中のH⁺濃度をもとに定義されており、

\(pH=-\log _{10}[H^{+}]または[H^{+}]=1.0\times 10^{-pH}\)

という式が成立している。

練習問題

1. 電離度α=0.050の酢酸水溶液の濃さが0.010mol/Lだったとする。\(\log _{10}5=0.70\)とし、この水溶液のpHを求めよ。
   
   
   
2. 0.1mol/LのNH₃が電離度0.010で水中で電離している。pHは？
   
   
   
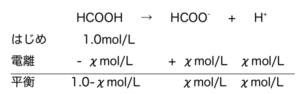
3. ギ酸の25℃での電離定数は\(K_{a}=2.8\times 10^{-4}\)である。1.0mol/Lのギ酸水溶液のpHはいくつか？ただし、\(\sqrt{2.8}=1.7、\log _{10}1.7=0.23\)とする。
   
   
4. アンモニア水における25℃での電離定数\(K_{b}\)は1.7×10^-5mol/Lである。0.1mol/Lのアンモニア水のpHはいくつか？ただ\(\sqrt{1.7}=1.3、\log _{10}1.3=0.11\)とする。
   
   
   

【解答】

1. CH₃COOH ⇄ CH₃COOH^– + H⁺ より、0.010mol/Lのうち割合0.050が電離してH⁺になることから、
   \([H^{+}]= 0.010\times 0.050= 5.0\times 10^{-4} mol/L \)
   \(∴pH= -\log_{10} (5.0\times 10^{-4}) \)
   \(=-\log_{10} 10^{-4} – \log_{10} 5.0 \)
   \(=4- \log_{10}5 =3.3\)
   
   
   
2. NH₃ + H₂O ⇄ NH₄⁺ + OH^–より、 
   \([OH^{-}]= 0.10\times 0.010= 1.0\times 10^{-3}mol/L\)
   ここで、水のイオン積より
   \([H^{+}]= \frac{K_{w}}{[OH^{-}]} = 1.0\times 10^{-11}mol/L\)
   \(∴pH= -\log_{10} (1.0\times 10^{-11}) = 11 \)
   
   
   
3. 
   
   

   式2

   
   より、平衡定数に代入し、
   \(\frac{x^{2} }{1-x} = K_{a} = 2.8\times 10^{-4} \)
   
   ここで、1-χ≒1と近似すると、χ²=2.8×10^-4よりχ=1.7×10^-2となる。
   
   これは実際1と2ケタ違うので1-χ≒1の近似は成立している。
   よって
   \([H^{+}]= 1.7\times 10^{-2} \)
   より、
   \(pH= -\log_{10}(1.7\times 10^{-2}) = 1.77\)
   
   
   ※オストワルトの希釈律よりとしても良いが、しっかりαも計算し、1-α≒1と近似できることを確かめてからでないと使ってはいけない。
   
   
   
4. NH₃ + H₂O ⇄ NH₄⁺ + OH^–より、オストワルトの希釈律を使うことを試みる。
   いま、\(α=\sqrt{\frac{K_{b}}{C}} = 1.3\times 10^{-2} \)より2ケタ異なるので、1-α≒1と近似できる。
   よって、
   \([OH^{-}]=\sqrt{CK_{b} = 1.3\times 10^{-3}}\)
   と計算できる。
   いま、水のイオン積は25℃で\(K_{w}= 1.0\times 10^{-14}\)より、
   
   \([H^{+}]= \frac{K_{w}}{[OH^{-}]} = \frac{1}{1.3} \times 10^{-11} mol/L \)
   \(∴pH= -\log_{10} (\frac{1}{1.3} \times 10^{-11})\)
   \(11 -\log_{10} \frac{1}{1.3} \)
   \(11+ \log_{10} 1.3 = 11.11\)

※pH指示薬の正体

BTB液やフェノールフタレイン液のようにpHの変化に伴って色の変わる指示薬の正体は、多くの場合弱酸またはその塩である。弱酸は

HA ⇄ H⁺ + A^–

と電離平衡状態になっており、酸性になるとH⁺濃度が上がるため、ルシャトリエの原理より平衡が右に移動する。
また塩基性になると、反対にH⁺濃度が下がり、左に平衡が移動する。
よって、A^–が色のついた物質なら酸性で呈色する指示薬になりうるし、HAが色の付いた物質なら塩基性で呈色する指示薬になりうる。
いま、平衡定数の式をたてると

\(\frac{[H^{+}][A^{-}]}{[HA]} = (一定) \)

となり、pHが1変わると[H⁺]が10倍変化するため、\(\frac{[A^{-}]}{[HA]}\)の割合も10倍変わる。
したがって、片方に色が付いているとpHが1変化するだけでも色は大きく変わるのだ。

★発展　※薄い酸のpH

たとえば1.0×10^-2mol/LのHClはpH2であるが、これを水で10倍に薄めると、H⁺濃度が1/10になるため、pHは3となる。
では、水で10倍、10倍…とどんどん薄めていくとpHは2→3→4→…となって8や9の塩基性になるのだろうか。
直感から明らかなように、HClをいくらうすめてもpHは7を超えて塩基性になることはない。
それはなぜかというと、HCl中のH⁺濃度が小さくなっていき、1.0×10^-6、1.0×10^-7、レベルになるとH₂Oの電離によって生じたH⁺の影響も無視できなくなるからである。

いま、1.0×10^-2mol/LのHClaqを考える。

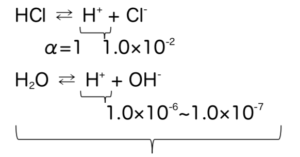
式3

本当はこの2つの電離を考えて、総H⁺濃度を考えるべきだが、濃い酸の場合、4ケタほど差が開くため、1.0×10^-2 + 1.0×10^-6 ≒ 1.0×10^-2 と水の電離の影響を無視できる。

しかし濃さが1.0×10^-6mol/Lレベルの酸になると水のH⁺も考えなくてはならない。

• Ex)1.0×10^-5mol/LのHClを水で1000倍にうすめるとpHはいくつか？
  
  

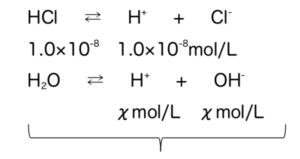
式4

H⁺はHCl由来の1.0×10^-8mol/Lと、H₂O由来のχmol/Lから成るとすると、水のイオン積から

\([H^{+}][OH^{-}]= 1.0\times 10^{-14}\)
\((x+ 10^{-8})・x= 1.0\times 10^{-14}\)

いま、

\(x ≒ 1.0 \times 10^{7}\)

より、

\( x+10^{-8}・x – 1.0\times 10^{-14} =0 \)

\(∴x= 0.95 \times 10^{-7}mol/L \)

これより、総H⁺濃度は

\([H^{+}]= 0.95\times 10^{-7} + 1.0\times 10^{-8} = 1.05\times 10^{-7} mol/L \)

\(pH= -\log_{10} (1.05\times 10^{-7})\)

\(=7-\log_{10}1.05 ≒ 6.98 \)

※7は超えない！

塩の加水分解と平衡

3章で見たように、弱酸+強塩基の中和反応で生成した塩の水溶液は塩基性を示し、強酸+弱塩基の中和反応では生成した塩の水溶液は酸性を示す。
その理由をここで詳しく見ていく。
たとえば、酢酸と水酸化ナトリウム水溶液の中和によってできた塩CH₃COONaは水に溶かすと塩基性を示すが、これはまず塩は完全に水中で電離することから

CH₃COONa → CH₃COO^– + Na⁺

そして、酢酸は弱酸であるから、電離度αは小さく、水中のH⁺と酢酸イオン

CH₃COO^– + H⁺ ⇄ CH₃COOH

が結びつき、酢酸に戻ることがある。よってこれらを合わせると、塩が

CH₃COO^– + H₂O → CH₃COOH + OH^–

という平衡状態にあることが分かる。
これを塩の加水分解といい、いまOH^–が発生していることから弱塩基性を示す。
なお、 OH^–がNa⁺と結びついてNaOHに戻らないのはNaOHが強塩基でα=1だからである。

　図解すると図2のようになる。

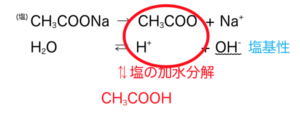
図2

★やや発展)では、このように塩を溶かした水溶液のpHを考えてみよう。
　いま、塩の加水分解の平衡

CH₃COO^– + H₂O → CH₃COOH + OH^–

　の平衡定数は、いつも通りH₂Oのモル濃度を一定とみなすことで、

\(\frac{[CH_{3}COOH][OH^{-}]}{[CH_{3}COO^{-}]} = (一定) =K_{h}\)

　　　　　　　　　　　　　　　　　　　　　　　　　※hydrolysisより
　となる。

この\(K_{h}\)を加水分解定数という。

ここで、酢酸の酸解離定数\(K_{a}\)は

\(K_{a} = \frac{[CH_{3}COO^{-}][H^{+}]}{[CH_{3}COOH]}\)

CH₃COOH ⇄ CH₃COO^– + H⁺

であったから、\(K_{a}・K_{h}=K_{w}\)をみたす。よって、加水分解定数は一般に、

\(K_{h}=\frac{K_{w}}{K_{a}}\)

となることが知られている。

• Ex)濃度Cmol/LのCH₃COONaの水溶液のpHは？

まず、CH₃COONa → CH₃COO^– + Na⁺ はα=1の電離なので、
[CH₃COO^–] = C mol/L である。すると、

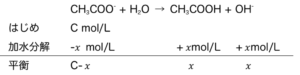
式5

           
より、平衡定数を考えて、

\(\frac{x^{2}}{C-x}=K_{h}\)

いま、加水分解によって戻るmol/LはCに比べて極めて少ないので、

\( ∴[OH^{-}] = x = \sqrt{CK_{h}} \)

※オストワルトの希釈律で見覚えある形！

よって

\([H^{+}]=\frac{K_{w}}{[OH^{-}]} = \frac{K_{w}}{\sqrt{CK_{h}}}\)

いま、

\(K_{h}=\frac{K_{w}}{K_{a}}\)

であるから、

\([H^{+}]=\frac{K_{w}}{\sqrt{\frac{CK_{h}}{K_{a}}} } = \sqrt{\frac{K_{a}K_{w}}{C}}\)

となり、pHを求めることができる。

緩衝液とpH

少量の酸や塩基を加えてもpHがあまり変化しない溶液を緩衝液という。
ヒトの血液など、急に変化してしまうと困るものはこれであることが多い。
一般に、

・弱酸 + その塩の混合溶液
・弱塩基 + その塩の混合溶液

は緩衝液になる。

たとえば、CH₃COOHとCH₃COONaの混合溶液を考えてみる。
いま、水中なのでCH₃COONaは完全に電離しており、CH₃COO^–とNa⁺に分かれている。

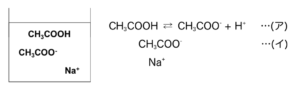
図3

1.  少量のHClを入れてみると…？
   →溶液中に大量に存在するCH₃COO^–(イ)とHClのH⁺が中和してCH₃COOHになるため、H⁺濃度に大きな変化はなく、pHはおよそ一緒のまま。
   
   
   
2. 少量のNaOHを入れてみると…？
   →加えたOH^–は、(ア)の右辺のH⁺と中和反応して打ち消される。具体的には、
   CH₃COOH + OH^– → CH₃COO^– + H₂O
   
   という反応により、(ア)の右向きがすすむだけでOH^–濃度に大きな変化はなくpHはおよそ一緒のまま。

このように①、②によって(ア)と(イ)が混在しているおかげで、酸・塩基を少量加えても打ち消せる緩衝液になっている。

★やや発展　※緩衝液のpHの計算

再びCH₃COOHとCH₃COONaの混合溶液について考えてみる。
いま、先述したようにCH₃COONaはCH₃COO^– + Na⁺に電離しており、CH₃COOHは
CH₃COOH ⇄ CH₃COO^– + H⁺という平衡状態にある。
そして、pH計算に必要な[H⁺]を含む式というと

\(K_{a}=\frac{[CH_{3}COO^{-}][H^{+}]}{[CH_{3}COOH]}\)

しかないが、ここで
[CH₃COOH]は、はじめに加えたCH₃COOHの初期濃度、
[CH₃COO^–]は、はじめに加えたCH₃COONaの初期濃度
を代入して計算して良い。
これはつまりCH₃COOHの電離している影響はきわめて小さいので考えなくて良いということである。
実際、CH₃COOHは弱酸であり、電離後の生じるはずだったCH₃COO^–はすでに大量にいるので、ほぼ電離していないため、\(K_{a}\)におけるモル濃度は初期濃度と考えて良さそうである。
よって\(K_{a}\)の式を変形し、

\([H^{+}]=\frac{[CH_{3}COOH]}{[CH_{3}COO^{-}]}K_{a}\)

となるため、緩衝液のpHは

\(pH=-\log(\frac{[CH_{3}COOH]}{[CH_{3}COO^{-}]}K_{a})\)

\(= -\log K_{a} – \log \frac{[CH_{3}COOH]}{[CH_{3}COO^{-}]} \)

となる。この式をヘンダーソン=ハッセルバルヒの式という。

(なお、少量の酸・塩基を加えた時のpHはその都度中和により変化する[CH₃COOH]と[CH₃COO^–]を計算して地道に求めていくしかない。)

• Ex)アンモニアの電離NH₃ + H₂O ⇄ NH₄⁺ + OH^–における電離定数\(K_{b}\)は\(K_{b}=2.0\times10^{-5}mol/L\)として、0.10mol/Lのアンモニア水100mLにNH₄Cl 0.010molを加えた水溶液のpHwp求めよ。
  ただし、\(\log_{10}2=0.30\)、\(\log_{10}3=0.48\)、溶液の体積はNH₄Clを加えても変化しなかったものとする。

であり、

緩衝液なので、この初期濃度を\(K_{b}\)の式に代入し、

よって、

なので、

\(∴pH= -\log(5.0\times10^{-10})\)
\(=10-\log5\)
\(=10-(\log\frac{10}{2})\)
\(=10-(\log10-\log2)=9.3\)

溶解度積

溶解度積とは

AgNO₃に HCl溶液を加えると、AgClという水に非常に溶けにくい塩が生成する。
この塩はごく少量なら水に溶け、飽和溶液になるとAgClという形で沈殿する。
そのため、沈殿が存在している時には、溶けているイオンと沈殿の間に以下のような溶解平衡が成立する。

AgCl (沈殿) ⇄ Ag⁺ + Cl^–

この平衡定数を考えると、

\(\frac{[Ag^{+}][Cl^{-}]}{[AgCl(沈)]}=(一定)\)

となるが、AgClの沈殿は固体であるため、モル濃度は一定とみなすことで定数に組み込んで、

\([Ag^{+}][Cl^{-}]=(一定)=K_{sp}\)

※spはsolubility product より

となる。この\(K_{sp}\)は溶解度積といい、沈殿に対して固有の値である。

※なお、このような難溶性塩はAgCl、CdS、ZnSなどが有名。詳しくは第2節の無機化学で扱う。

難溶性塩の沈殿判定法

MX(沈)⇄M⁺ + X^–の溶解平衡が成り立っており、溶解度積を\(K_{sp}\)とすると

\([M^{+}][X^{-}]>K_{sp}\)　→ 沈殿が生じており、
\([M^{+}][X^{-}]=K_{sp}\)　となるまで沈殿が生じる。
\([M^{+}][X^{-}]<K_{sp}\)　→すべてが溶けており、沈殿はない。
いわば、\(K_{sp}\)は溶けきれるギリギリのラインのことである。

分かりにくいので具体的にAgClで見てみる。
AgClの\(K_{sp}\)は、25℃で[Ag⁺][Cl^–]=1.8×10^-10mol²/L²=\(K_{sp}\)である。
 たとえば水に1LにAg⁺を2.0×10^-3mol、Cl^–を3.0×10^-5mol入れたとすると、
[Ag⁺][Cl^–]=6.0×10^-8mol²/L²\(>K_{sp}\)となるため\(K_{sp}\)を超えており、溶けられる限界を超えてしまっている。
すなわち、沈殿が生成している。

一方、水1LにAg⁺を2.0×10^-10、Cl^–を3.0×10^-12mol入れたとすると、
[Ag⁺][Cl^–]=6.0×10^-8mol²/L²\(<K_{sp}\)となるため、限界値の\(K_{sp}\)を超えておらず、すべてのAg⁺とCl^–は水に溶けている。

さらにAg⁺とCl^–を添加しても、\(K_{sp}\)に達するまでは溶けることができる。

このように\(K_{sp}\)は溶解と沈殿の境となる基準として大変重要である。

また、いま見たように[Ag⁺][Cl^–]=\(K_{sp}\)はAgClの沈殿がある際には保たれているため、そこにさらにHClを加えると[Cl^–]が大きくなるので、[Ag⁺]を減らさないと積が一定を保てず、AgClの沈殿生成が促進される。

このように、同種のイオンを加えて平衡を移動させる、ルシャトリエの原理のような現象を、共通イオン効果という。

Ag⁺ + Cl^– ⇄ AgCl (沈)
[Ag⁺][Cl^–] =\(K_{sp}\)

↑ 添加すると、AgClの沈殿が生成されていく。

 練習問題

難溶性塩のBaSO₄の飽和溶液100mL中には、BaSO₄が2.33×10^-4g溶解している。ただし、Ba=137、S=32、O=16とする。

1. BaSO₄の溶解度積はいくらか？
   
   
2. 0.050mol/LのH₂SO₄1LにBaSO₄は最大何gまで溶解するか？

【解答】

1. BaSO₄は式量233より、飽和溶液100mLに1.0×10^-6mol溶けている。
   よって、BaSO₄のモル濃度は1.0×10^-6mol/0.1L=1.0×10^-5mol/Lである。
   ところで飽和溶液では[Ba⁺][SO₄^2-]=\(K_{sp}\)を満たすことから、
   
   1.0×10^-5×1.0×10^-5=1.0×10^-10mol²/L²
   
   
   
2. まず、すでにこの溶液中には[SO₄^2-]=0.050mol/Lが存在している。
   そしてBaSO₄を限界まで溶かした時、限界ということは溶解と沈殿の境であるから、
   [Ba⁺][SO₄^2-]=\(K_{sp}\)を満たさねばならない。
   いまBaSO₄を\(xmol/L\)溶解させた時、[Ba⁺]=\(xmol/L\)、[SO₄^2-]=\(xmol/L\)で溶けることから、
   \(K_{sp}\)の式に代入し、
   
   \(x(x+0.050)=1.0\times10^{-10}mol^{2}/L^{2}\)
   が成り立つはず。
   
   ここで\(x<<0.050\)と考え、\(x+0.050≒0.050\)とすると、

\(x\times0.050≒1.0\times10^{-10}\)

より、\(x=2.00\times10^{-9}mol/L\)

この\(x\)は確かに\(x<<0.050\)であるから正しく、

\(2.00\times10^{-9}\times233=66\times10^{-7}g\)

　※電離平衡問題の一般的解放(発展)

例えば

『0.100mol/LのCH₃COOHのpHを求めよ。ただし、酸解離定数\(K_{a}=1.75\times10^{-5}mol/L\)とする。』

という問題があったとする。

この章で扱った方法で解くならば、オストワルトの希釈律から

\([H^{+}]=\sqrt{CK_{a}}
=\sqrt{0.100\times1.75\times10^{-5}}
=1.32\times10^{-3}mol/L\)

\(∴pH=-\log(1.32\times10^{-3})≒2.88\)

と求められる。

よって\(1-α≒α\)と近似可能。

しかし、この方法で解くのは実は高校生までである。なぜなら、電離を1回しかない弱酸・弱塩基が単独で存在している時にしか使えないというように非常に限定的な条件下でしか使えないからである。どのような溶液でも[H⁺]を考えられるように大学生以降では以下のような方法で計算していく。

おおまかな方針としては

1. 物質量保存の式
2. 電荷保存の式
3. 平衡定数の式

の3式をたてて連立することによって計算する。

この問題なら、CH₃COOH ⇄ CH₃COO^– + H⁺より、

1. 物質量保存の式
   入れたCH₃COOHは一部電離していることから、入れた分の濃度は分かれて存在し
   
   [CH₃COOH]+[ CH₃COO^–]=0.100mol/L
   
   
   
2. 電荷保存の式
   溶液中の+イオンと-イオンの数はつり合いが取れて±0になっており、
   
   [CH₃COO^–]+[OH^–]=[H⁺]
   
   
   
3. 平衡定数の式
   
   
   \(\frac{[CH_{3}COO^{-}][H^{+}]}{[CH_{3}COOH]}=1.75\times10^{-5}mol/L\)

の3式を連立する。未知数が[CH₃COOH]、[CH₃COO^–]、[H⁺]、[OH^–]の水のイオン積の式を合わせたら4式あるので解くことができる。

②式より[CH₃COO^–]=[H⁺]-[OH^–]、①式より[CH₃COOH]=0.100-[CH₃COO^–]=0.100-([H⁺]-[OH^–])

なので、これらを③式に代入して、

\(\frac{([H^{+}]-[OH^{-}])[H^{+}]}{0.100-([H^{+}]-[OH^{-}])}=1.75\times10^{-5}\)

　ここに水のイオン積を代入し、[H⁺]に関する3次方程式を解くことでも求められるが、

いま酸性溶液なので[H⁺]≫[OH^–]とみなし、[H⁺]-[OH^–]≒[H⁺]と近似すると

\(\frac{[H^{+}]^{2}}{0.100-[H^{+}]}=1.75\times10^{-5}\)

 この[H⁺]に関する2次方程式を解いてもよいが、CH₃COOHは弱酸なので0.10≫[H⁺]とみなすと0.100-[H⁺]≒0.100と近似することができ、

\([H^{+}]^{2}=1.75\times10^{-5}\times0.100\)

\(1.75\times10^{-5}→K_{a}\)
\(0.100→C\)

\([H^{+}]=\sqrt{CK_{a}}\)と同じ

\(∴[H^{+}]=1.32\times10^{-3}mol/L\)

\(pH=-\log(1.32\times10^{-3})≒2.88\)

京大等でこの解き方も出題されているので興味のある人はぜひ手を動かしてみてほしい。

なお、この方法なら2価の弱酸水溶液のpHも計算することができる。
以下の内容は大学1~2年レベルの計算であり、高校生が解ける必要はないが、大学生以降は「分析化学」という分野でこのような化学計算をしているのだ、と感じてもらえるといいと思う。

練習問題(発展)

1.00×10^-3mol/Lの2価の弱酸水溶液のpHを求めよ。
ただし、1段階目の電離定数は1.12×10^-3mol/L、2段階目の電離定数は3.91×10^-6mol/Lとする。

【解答】

H₂A ⇄ HA^– + H⁺
HA^– ⇄ A^2- + H⁺

1. 物質量保存の式
   [H₂A] + [HA^–] + [A^2-] = 1.00×10^-3mol/L
   
   
   
2. 電荷保存の式
   [H⁺] = [OH^–] + [HA^–] + 2[A^2-]
   
   
   
3. 平衡定数の式
   \(\frac{[HA^{-}][H^{+}]}{[H_{2}A]}=K_{a1}\)、
   \(\frac{[A^{2-}][H^{+}]}{[HA^{-}]}=K_{a2}\)

の3種類の式がまず立つ。未知数は[H₂A]、[HA^–]、[A^2-]、[H⁺]、[OH^–]の5つで、
水のイオン積を合わせるといま5式あることからそれぞれを求めることができる。

まずは①式をもとに考えていく。③式を用いて、①式は以下のように表される。

①より、

\(\frac{[HA^{-}][H^{+}]}{K_{a1}}=[HA^{-}]+\frac{[HA^{-}]K_{a2}}{[H^{+}]}=1.00\times10^{-3}mol/L\)

※[HA^–]でくくると

\(↔︎\frac{[H^{+}]^{2} + [H^{+}]K_{a1}+ K_{a1}K_{a2}}{[H^{+}]K_{a1}}\times[HA^{-}]=1.00\times10^{-3}mol/L\)

\(∴[HA^{-}]=1.00\times10^{-3}\times \frac{[H^{+}]K_{a1}}{[H^{+}]^{2} + [H]^{+}K_{a1}+K_{a1}K_{a2}}\)

と変形でき、[HA^–]を[H⁺]で表せる。1変数消去の準備ができた。

同じようにして、①式と③式から[A^2-]を[H⁺]で表してもう1変数消去の準備を行う。

③の2式をかけ合わせると

\(\frac{[A^{2-}][H^{+}]^{2}}{H_{2}A}=K_{a1}K_{a2}\)

となることを用いて、

①より、

\(\frac{[A^{2-}][H^{+}]^{2}}{K_{a1}K_{a2}} + \frac{[A^{2-}][H^{+}]}{K_{a2}} + [A^{2-}] =1.00\times10^{-3}mol/L\)

\(↔︎\frac{[H^{+}]^{2} + [H^{+}]K_{a1}+ K_{a1}K_{a2}}{K_{a1}K_{a2}}\times[A^{2-}]=1.00\times10^{-3}mol/L\)

\(∴[A^{2-}]=1.00\times10^{-3}\times \frac{K_{a1}K_{a2}}{[H^{+}]^{2} + [H]^{+}K_{a1}+K_{a1}K_{a2}}\)

よって、これらを②式に代入することで

\([H^{+}] = [OH^{-}] +1.00\times10^{-3}\times (\frac{[H^{+}]K_{a1}}{[H^{+}]^{2} + [H^{+}]K_{a1} + K_{a1}K_{a2}} + \frac{2K_{a1}K_{a2}}{[H^{+}]^{2} + [H^{+}]K_{a1} + K_{a1}K_{a2}})\)

いま、この式に水のイオン積(\([OH^{-}]= K_{w}/[H^{+}]\))を代入することで得られる4次方程式をパソコンで解いてもよいが、弱酸なので\([H^{+}]>>[OH^{-}]\)であるから\([H^{+}]-[OH^{-}]≒[H^{+}]\)と近似して、

\([H^{+}] = 1.00\times10^{-3}\times \frac{[H^{+}]K_{a1} + 2K_{a1}K_{a2}}{[H^{+}]^{2} + [H^{+}]K_{a1} + K_{a1}K_{a2}}\)

分母をはらって

\([H^{+}]^{3} + K_{a1}[H^{+}]^{2} + K_{a1}(K_{a2} – 10^{-3})[H]^{+} -2K_{a1}K_{a2}\times10^{-3}=0\)

この3次方程式を解いてもいいが、近似をうまく使っていくと2次方程式に落としこめる。

\(K_{a2}=3.91\times10^{-6}\)より\(K_{a2}<<10^{-3}\)であるため、\(K_{a2} – 10^{-3}≒ -10^{-3}\)と近似し、

\([H^{+}]^{3} + K_{a1}[H^{+}]^{2} – K_{a1}\times 10^{-3}\times [H]^{+} -2K_{a1}K_{a2}\times10^{-3}=0\)

\(↔︎[H^{+}]^{3} + K_{a1}[H^{+}]^{2} – K_{a1}\times 10^{-3}\times ([H^{+}]+ 2K_{a2})=0\)

ここで、弱酸は[H⁺]=10^-3~10^-4程度と考え、 \([H^{+}]>>2K_{a2}\)であるから、

\([H^{+}] + 2K_{a2} ≒[H^{+}] \)

と近似すると、

\([H^{+}]^{3} + K_{a1}[H^{+}]^{2} – K_{a1}\times 10^{-3}\times [H^{+}]=0\)

よって [H⁺]で割ることにより以下の2次方程式を得る。

\([H^{+}]^{2} + K_{a1}[H^{+}] – K_{a1}\times 10^{-3}\times [H^{+}]=0\)

\(∴[H^{+}]=6.37\times 10^{-4}\)

よって

と求まる。
近似の便利さをよく見て感じてほしい。

おすすめ記事

• 3.酸塩基反応〜中和反応の量的関係を利用できるようになろう〜[大学受験化学-理論化学]
• 10.反応速度と化学平衡①〜実験データから反応速度式を求めよう〜[大学受験化学-理論化学]

参考

• 卜部吉庸、『化学の新研究　改訂版』、三省堂、2019