前回に引き続き，力の種類について見ていこう．
Contents
公式のある力
摩擦力
摩擦力には3 種類の言葉があり，混乱しがちなので，まずはそれぞれをおさえよう．摩擦力には静止摩擦力，最大摩擦力，動摩擦力の3 つがあり，静止摩擦力には公式がないが，最大摩擦力と動摩擦力には公式がある．
静止摩擦力は例えばざらざらした斜面上の物体が静止しているとき，滑らないように働いている力が静止摩擦力である．これをどんどん傾けていき，斜面がある角度に達すると物体が滑り出す．この滑り出す直前で，物体を静止させるように働いている摩擦力が最大摩擦力である．そして滑り出した物体にもざらざらした斜面から運動を妨げる向きに摩擦力が働き，これが動摩擦力である．
日常的にもこれらの摩擦力を感じる経験があると思う．例えば，床に置いてある何か重い荷物を押して移動させることを考えよう．最初の押しはじめでは荷物がぴくりとも動かない．これが静止摩擦力の影響である．さらにもっと力を加えていくと，あるところで動き出す．このときが最も力を加えているときで，これに対抗する力が最大摩擦力である．
そして1 度荷物が動いてしまうと，それほど力を加えなくても物体を動かし続けることができる．このときに床からの荷物に働いている力が動摩擦力である．
これらの最大摩擦力と動摩擦力は実験から垂直抗力の大きさ\(N\)に比例することが分かっている．よって最大摩擦力は
\(F = \mu N\) (1)と書かれ，動摩擦力は
\(F = \mu ‘N\) (2)と書かれる．ここで\(\mu\)1は静止摩擦係数，\(\mu’\)は動摩擦係数という．静止摩擦係数は静止摩擦力を求めるのには使わないので注意してほしい．
浮力
水に木片を浮かべたり，気球が浮かんだりするのは浮力が働くからである．浮力は液体や気体といった流体中の物体に働く力である．この浮力がどうして生じるのかを見ていく．そのためにまず圧力について見る．
圧力とは「力」という字が入っているが，圧力は力ではない．この圧力は特に流体を扱うような場合に重要になる．というのも質点と違い流体は広がりを持つからである．圧力の定義は単位面積あたりに働く力である．それを式で表そう．ある力\(F\)が面積\(S\)の面に働いているとき，圧力\(P\)は，
\(P = \frac{F}{S}\) (3)である．
では浮力の説明に入ろう．浮力は物体が流体から受ける圧力による力の差によって生じる．そのことを以下の図1 を参照しながら式を導こう．今，密度\(\rho _{m}\)で底面(上面と下面)の面積が\(S\)で，高さ\(h\)である物体が密度\(\rho\)の流体中にあり，圧力を受けていることを考える．
ところで水に深く潜れば深く潜るほど圧力を感じる．これは深く潜るほど自分の上にのしかかる水の量が増えるからである．つまり，流体中の圧力は流体の重力に起因しているのである．
まず図1 において，物体の上面に働く圧力\(P(x)\)を考える．圧力は物体の上面に乗っかっている流体の重力を上面の面積で割ったものである．実際に計算すると，
\(P(x) = \frac{\rho Sxg}{S} = \rho gx\) (4)となる．
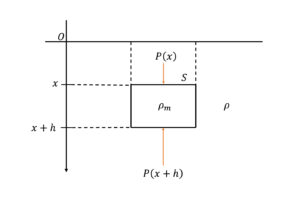図1: 密度m，底面の面積が\(S\)，高さ\(h\)であるの物体が密度 の流体中にあり圧力を受けている．水面は(\(x = 0\)) である．
次に物体の側面に働く圧力を考える．これは結果から述べると，側面に働く圧力は考慮しなくて良い．物体を流れのない流体中に沈めたとき，自然に左右に動くことはない．これは側面に働く流体の圧力の大きさが等しく，打ち消し合うからである．深くなればなるほど(\(x\)が大きくなるほど) 圧力が大きくなるということからも分かるように，同じ深さでの圧力は等しい．だから側面からの圧力は相殺する．
最後に下面に働く圧力を考えよう．下面での圧力は上面の圧力と深さが異なるだけなので，
\(P\left( x+h\right) = \rho g\left( x+h\right)\) (5)
となる．
以上より，下向きが正の向きであることに注意すると，上面と下面の圧力による力の差2は，
\(-\left[ P\left( x+h\right) -P\left( x\right) \right]S = -\rho Shg = -\rho Vg\) (6)となる．ここで\(V = Sh\)は物体の体積である．結果にマイナスがついていることから上向きの力であることが分かる．
よって，浮力の大きさの公式は，
\(F = \rho Vg\) (7)である．注意してほしいことは，浮力の公式自体には物体の密度\(\rho m\)は含まれず，物体の周囲の密度 が寄与するということである．
ここまでで浮力の公式が導けたが，ある物体が浮かぶかどうかについて考えてみよう．図1 の物体に働いている力は先ほど求めた浮力と重力である．もし重力の方が大きければ沈むし，浮力の方が大きければ浮くことになる．したがって物体が浮かぶためには(浮力)>(重力) という大小関係であれば良いので，
\(\rho Vg < \rho_{m}Vg\) (8)となるから，
\(\rho < \rho_{m}\) (9)となり，物体の密度が流体の密度より小さければ浮かぶことが分かる．これは経験的によく知っていることだろう．水に木片を入れれば浮かぶし，鉄を入れれば沈む．
クーロン力
以下では電磁気学で登場する力の公式を挙げる．冒頭でも述べたように，詳細は電磁気学の部分で学んでほしい．(電磁気学未習の場合は，とりあえずこんなものがあるのか程度に読んでほしい．)
今，以下の図2 のように2 つの点電荷\(q_{1}\)，\(q_{2}\)が距離\(r\)を隔てて存在しているとき，それらの間にクーロン力が働き，その大きさ\(F\)は，
\(F = k\frac{q_{1}q_{2}}{r^{2}}\) (10)である．ここで\(k\)はクーロン定数で，
\(k = 8.99\times 10^{9}Nm^{2}/C^{2}\) （11)という値を持つ．
点電荷の符号が同符号(\(q_{1}q_{2} > 0\)) のときは斥力(反発力) で，異符号(\(q_{1}q_{2} < 0\)) のときは引力である．また作用反作用の法則から，2 つの点電荷に働く力は同じ大きさで逆向きである．
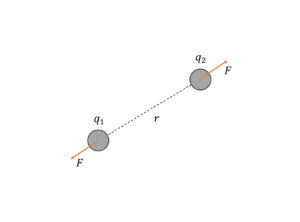図2: 2 つの点電荷\(q_{1}\)，\(q_{2}\)が距離\(r\)を隔てて存在しているとき，それらの間にクーロン力が働く．
ローレンツ力
磁束密度\(B\)の中を電荷\(q\)の点電荷が速さ\(v\)で運動しているとき，点電荷にはローレンツ力が働き，その力の大きさは，
\(F = qvB_{n}\) (12)である．ただし\(B_{n}\)は磁束密度の速度に垂直な成分である．
アンペール力(電流が磁場から受ける力)
磁束密度\(B\)中に電流\(I\)が流れている長さ\(l\)の導体があるとき，アンペール力(電流が磁場から受ける力) が働き，その大きさは，
\(F = IB_{n}l\) (13)である．ただし\(B_{n}\)は磁束密度の電流に垂直な成分である．
(発展) 力の種類は4つ
4 つの力
ここでは受験とは関係なく興味のある人向けの話を述べる．今まで「力の種類」という題名で多くの力を紹介した．ここまで読むと，力にはもっと種類があるのではないか，と思う人もいるかもしれない．しかし実はこの世には力は4 種類しか存在しない．その力とは，重力，電磁気力，強い核力，弱い核力である．しかも後ろの2 つは基本的には高校では習わない3．では今までのたくさんの力は何なのだと思うのが当然だろう．
今まで登場した力について詳しく見ていこう．はじめに登場した重力と万有引力は同じものであることは既に述べた．そして実はそれ以降に登場した力は全て電磁気力である．最後の方に登場した力は電磁気的な力であることは疑いもないだろう．では弾性力や摩擦力はどうして電磁気学的な力なのか．これは物体をもう少し小さい視点で見ると分かる．
物体を構成しているのは原子である．原子は中心に原子核が存在し，その周りに電子が存在している．物体がこすれ合うとき，小さい視点で見るとこの外側にある電子同士がぶつかるのである．この電子同士は互いに反発し合うので摩擦力が生じる．弾性力の元に戻ろうとする力も原子同士の結びつきによるものである．このように考えると身の周りのほとんどの物理現象は電磁気力の結果であることが分かる．
重力は弱い
さてここで重力と電磁気力の「強さ比べ」をしよう．重力と電磁気力のどちらが強いのか．自分がジャンプしてもすぐに着地してしまうことから重力が強いと思う人もいるかもしれないが，電磁気力の方が圧倒的に強いのである．例えば下敷きを布でこすって静電気を帯びさせ，髪の毛を逆立てた経験のある人も多いのではないだろうか．静電気はもちろん電磁気力である．髪の毛が普段垂れているのは重力のためであるが，下敷きで簡単に重力に逆らって髪の毛を持ち上げることができてしまう．重力はやっと地球ぐらいの質量で髪の毛を引っ張っているのにも関わらず，である．頬杖がつけるのも，重力よりひじと机の電気的な反発力の方が強いからである．
この強さの違いは万有引力定数とクーロン定数の値を見ても分かる．桁数が全く違うことが分かるだろう．実は，残り2 つの強い核力や弱い核力と比べても重力はその名の通り桁違いに弱いのである．なぜだろうか．
少しだけ重力の話をしよう．重力はアインシュタインの一般相対性理論によって，「時空間の歪み」によるものだと分かった．これは(よくある例だが) ぴんと張ったゴムの膜にボールをのせるとへこむが，重いボールがあるとそのくぼみが深くなり，その周囲に別のボールを転がすとそのくぼみに引っ張られるように転がり込む．このようなことが起こっているというのである．これだけではよく分からないかもしれないが，要は「重力は時空間の性質によるもの」という意味で，他の力とは異なっているのである．
さて，この重力だけが弱い理由についてだが，現在も研究がなされているものである．重力だけが他の3 つとうまく調和しないので，それらを統一して説明できる理論が研究されているが，未だに完成した理論はない．興味のある人は本屋で調べたり，大学や大学院で勉強してみるのもよいだろう．
(発展) 逆2乗則と空間の次元について
ここでもうひとつ，余談をしよう．万有引力やクーロン力を習ったときに，「なぜ距離の2 乗に反比例するのか」という疑問が生じる人もるだろう．重力や電磁気力が従う「距離の2 乗に反比例する」法則を逆2 乗則という．これらは偶然の一致とは思えない．何か意味があるだろうと考えられる．この逆2 乗則だが空間が3 次元であることから来ているのである．そう言われてもすぐにはぴんと来ないだろう．
そこで次のような例を考えよう．ある光源があって，四方八方に光を放っている．この光の強さを距離r のところで調べよう．光源から発せられた光量は，距離\(r\)のところでは半径\(r\)の球面に広がるから，距離\(r\)での光の強さ\(L\)は
\(L ∝ \frac{1}{4\pi r^{2}}\) (14)である．ここで∝は比例を意味する記号である．これは空間が3 次元ならではの結果で，もし空間が2 次元だとしたら，球面ではなく円になるので，
\(L ∝ \frac{1}{2\pi r}\) (15)となり，言うなれば「逆1 乗則」になってしまう．このように逆2 乗則は空間の次元に依存しているのである．
ところがこの世界の空間は3 次元ではない(もっと高次元である) とする研究が現在もなされている．余剰次元があるとうまく理論が構成できるらしいのだ(筆者も詳しくは理解していない．)．このような次元を「余剰次元」と言ったりするが，現在実験的にそのような次元があることはまだ確かめられていないが，物理研究の大きな題材のひとつである．
1「ミュー」と読む．
2「力」なので面積をかけることを忘れないこと．
3原子物理学の単元で少しは習うかもしれない．
おすすめ記事
参考
こんにちは。慶應義塾大学大学院物理学科の花井遼介です。
中学から大学生の前半くらいまではバドミントンをずっとやっていましたが、途中から勉強や研究が忙しくなり、最近ほとんどやっていません。なかなか運動をする機会が減って残念ですが、時々自転車の乗って知らない場所に行ったり、散歩をしたりしています。(特に研究に行き詰ったとき……)昔から理科が好きで、高校生の時に聞いた、とある物理学者の講演に感動して以来、大学では物理を専門に学びたいと思っていました。現在は原子核理論の研究室に所属しています。その中でも僕は中性子星という超高密度な天体を、原子核理論の立場から研究しています。物理が好きでそれを専ら学んでいることもあって、高校生向けに高校物理や大学に入ってからの物理、物理学科についてなどの記事を提供していこうと思います。高校物理の記事でも、僕が大学に入って得た知識や理解をもとに、受験に役立つのみならず、学問としての面白さが含まれるような記事を書くつもりです。(受験向けの部分とそうでない部分は分かるように書くつもりですので、興味や必要に応じて読んでもらえればと思いま。)
僕の書く記事は、あくまで読者の皆さんの「補助的なもの」です。最終的には自分で勉強する、ということが大事になります。なので記事をきっかけに、皆さんが自分で物理を勉強できる状態になれれば、僕の目標は達成されたことになります。
僕の記事からさらに自分でもさらに深く勉強してほしいと思います。
皆さんと共に物理の面白さに触れ、理解を深められることを願っています。
