水溶液の性質を調べたり,水溶液に関する問題を解くうえで,その濃度を正確に知ることはとても重要なことになってきます.
特に学び始めの頃は濃度の計算について,その定義に誤解が生じやすいです.
ここでは水溶液の濃度を考えるうえで必要な知識とともに,正しい濃度の計算の方法,濃度に関連した種々の問題について紹介します.
Contents
水溶液の濃度1
まず最初に「水溶液の濃度とは何か」ということや,「どう計算すればよいか」を説明してしまいます.
小学校や中学校の理科で「濃度」と言うとき,少し難しい言葉でいえば「質量パーセント濃度」と呼ばれるものを指しています.
水溶液における「質量パーセント濃度」とは,「水溶液全体の重さ」を基準として「溶けている物質(塩や砂糖など)の重さ」が全体の何%の重さを占めているかを指します。
つまり「水溶液の濃度の計算式」は下のように書くことができます.
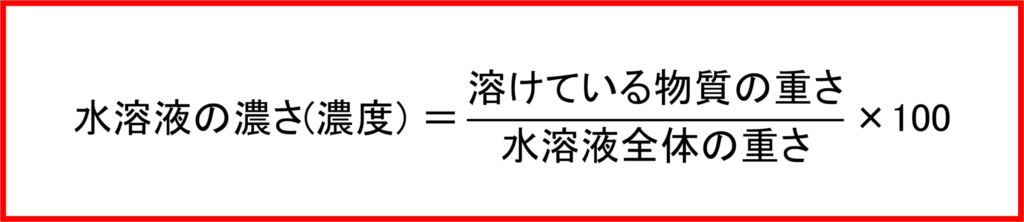
(例) 水溶液全体の重さが100gで,その中に食塩が20gだけ溶けているときの食塩の(質量パーセント)濃度
(溶けている食塩の重さ)÷(水溶液全体の重さ)=(20÷100)×100=20
答え:20%
濃度の計算では,百分率の計算や小数の計算がかなり多く出てくるので素早く計算できるように練習を重ねておきましょう.
水溶液の濃度2
上で簡単に水溶液の濃度について確認しましたが,実際は「水溶液全体の重さ」が問題でそのまま提示されることはほとんどありません. 水溶液の全体の重さは自分で求めなければいけない場合も多いです.
それでは多くの場合,水溶液の濃度を求める問題として多いのはどういうタイプかを見ていきましょう。
(例) 100gの水に食塩を20g溶かした食塩水は何%の濃さですか. 小数第2位を四捨五入しなさい.
まずは実際に解いてみてください.
ここでよくある間違いを紹介しましょう.
食塩の重さを水の重さで割り,
(20÷100)×100=20
つまり20%と計算した方は間違いです.
何が間違っているのかも含めて正しい解き方を確認しましょう.
上の解き方で誤っているのは,「水溶液の全体の重さ」(分母部分)です.
上の問題における「水溶液全体の重さ」は,「水の重さ+溶かした食塩の重さ」となります。
つまり,正しい計算式は,
{20÷(100+20)}×100=16.66…≒16.7
よってこの食塩水溶液の濃度は,正しくは約16.7%となります.
このように水の重さと溶かした物質の重さは基本的に別々に提示されるため,水溶液の濃度を求める計算式は下のように覚えたほうがよいでしょう.

「水の重さと溶けている物質の重さの合計」が「水溶液全体の重さ」となる点に特に注意しましょう.
物質が水に溶けるとは(発展)
物質を水に溶かしたとき,「水溶液全体の重さ」が「水の重さ+溶けている物質の重さ」となることをより直感的に分かりやすくするため,「物質が水に溶けるとはどういうことか」について少し詳しく見てみましょう.
ここでは食塩が溶けるときに起こっている現象を見てみましょう。
ただしこの節の文章や図にはイメージしやすさを優先した結果,厳密にいうと必ずしも正しいとは言えない表現がいくつかあります. 本当に気になる方は高校化学レベルの溶解や結晶について,自分で調べてみましょう.
食塩の粒は,主に「塩化ナトリウム」という物質の粒がいくつも集まってできています。

水も同じく「水」という物質の粒が集まってできているわけですが,食塩を水に入れると,水の粒が食塩の粒から塩化ナトリウムの粒を引っ張って,細かく分解されていきます.
水の粒によって次々と細かく分解された結果,最終的には私たちの目には見えない大きさになり,全体へ拡散するのです. これが基本的な「溶ける」という現象です.
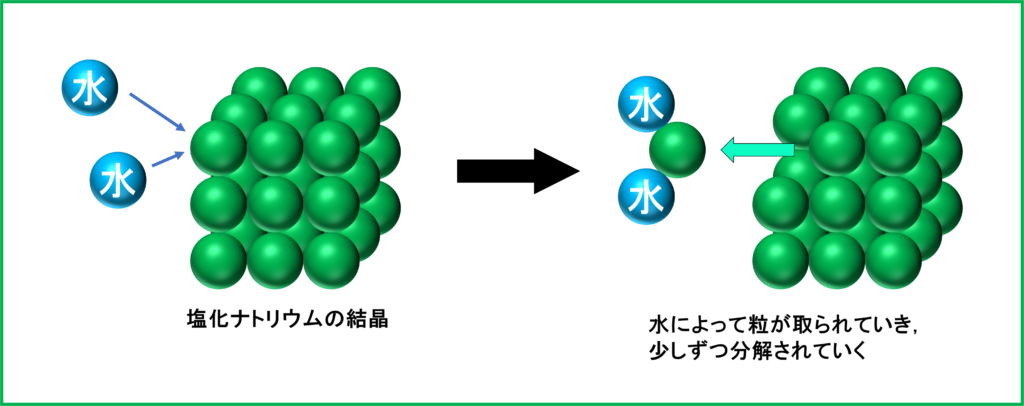
つまり,水に溶かした物質は見た目上はなくなっていても,実際には量は同じのまま,目に見えないほど細かくなっているだけなので,重さは水の重さに加えて,溶かした分がそのまま水溶液全体の重さとして加わることになるのです.
濃度の関連問題
それではここで濃度に関連した実際の問題をいくつか解いてみましょう.
問題

解答
1.
- (1) 26.3%
- (2) 食塩263g, 水737g
- (3) 163g
2.
- (1) 41.2%
- (2) 5g
解説
1
(1)
水溶液全体の重さが「水の重さ+溶かした食塩の重さ」であることに注意して計算すると,
35.7÷(100+35.7)×100=26.30…≒26.3
(2)
全体が1kg,つまり1000gであるから,その重さのうち26.3%が食塩であればいいから,食塩の重さは,
1000×0.263=263
つまり必要な食塩の重さは263gです.
残りの重さの分の水を入れればよいので,
1000-263=737
よって求める水の重さは737gです.
(3)
濃度26.3%の食塩水100gに含まれる食塩の重さは,
100×0.263=26.3
よって26.3g
今から水を加えて濃度10%の食塩水を作るから,26.3gが完成した水溶液の重さの10%であるとすると,今から作る水溶液の全体の重さは,
26.3÷0.1=263
最初にある食塩水溶液が100gだから,その差を計算して,
263-100=163
よって,水を163g加えればよいことになります.
2
(1)
水溶液全体の重さが「水の重さ+溶かした固体物質Aの重さ」であることに注意して計算すると,
70÷(100+70)×100=41.17…≒41.2
(2)
固体物質Bの濃度が20%ということは,固体物質Bが水溶液全体の重さの20%を占めているということです.
つまり,水の重さ100gは残りの80%を占めていることになります.
よって,溶けている固体物質Bの重さを□とすると,重さの比は
100:□=80:20=4:1
つまり□=25となり,溶けている固体物質Bの重さは25gということになります.
問題文より,固体物質Bは30gまで溶けるので,残り5g溶かすことができます.
入試問題演習
ここまでに学習した内容を活かして,実際の入試問題に挑戦してみましょう.
問題1


解答1
- 問1 エ
- 問2 イ
- 問3 3g
- 問4 37%
- 問5 36g
- 問6 イ,エ
解説1
問1
今,それぞれのビーカーに10℃の水が50gずつ入っているので,食塩とミョウバンがそれぞれ10℃の水50gに何gずつ溶けるかを調べます.
表1より,10℃の水「100g」に対して,食塩は36g,ミョウバンは8g溶けることが分かります.
今,水は100gの半分(0.5倍)の50gしかないので,溶ける食塩の量やミョウバンの量も半分(0.5倍)になります.
つまり10℃の水50gに対して,食塩は18g(36×0.5=18),ミョウバンは4g(8×0.5=4)溶けます.
今,10℃の水50gに対して,食塩もミョウバンも20gずつ入れようとしており,上で求めた最大の溶ける量を超えているので,どちらも溶けきることはありません.
したがってエが正解となります.
問2
問1と同じように考えます.
今,それぞれのビーカーに60℃の水が50gずつ入っている状態を考えればよいので,食塩とミョウバンがそれぞれ60℃の水50gに何gずつ溶けるかを調べます.
表1より,60℃の水「100g」に対して,食塩は37g,ミョウバンは58g溶けることが分かります.
今,水は100gの半分(0.5倍)の50gしかないので,溶ける食塩の量やミョウバンの量も半分(0.5倍)になります.
つまり60℃の水50gに対して,食塩は18.5g(37×0.5=18.5),ミョウバンは29g(58×0.5=29)溶けます.
今,60℃の水50gに対して,食塩もミョウバンも20gずつ入れている。食塩は溶ける最大の量18.5gを超えた20gですが,ミョウバンは溶ける最大の量29gより少ない20gとなっているので,食塩は溶け残りますが,ミョウバンは全て溶けきります.
したがってイが正解となります.
問3
まずは入れた食塩の重さを求めます.
問題文より,全体の重さ,つまり「ビーカーの重さ+水の重さ+食塩の重さ」が200gとなっています.
今,ビーカーの重さは60g,水の重さが100gなので,200-60-100=40より,食塩の重さは40gとなります.
ここで表を見ると,10℃の水100gに溶ける食塩の最大の量は37gです.
今,上の計算から食塩を40g入れたことが分かっているので,これは10℃の水100gに溶ける最大の量37gを3g(40-37=3)超えているため,その分だけ溶け残ります.
したがって溶け残った食塩は3gです.
問4
ろ過では,溶けきれなかった分のミョウバンが取り除かれます.
今,表から60℃の水100gにはミョウバンが最大58g溶けることが分かります.
問題で入れたミョウバンは60gなので,60℃の水100gに溶ける最大の量58gから超過した分の2g(60-58=2)はろ過で取り除かれることになります.
つまりろ過後の水溶液は,100gの水にミョウバン58gが溶けた状態となっています.
水溶液全体の重さは水の重さとミョウバンの重さを足し合わせた158g(100+58=158)なので,この水溶液の濃さ(濃度)は,(58÷158)×100=36.7≒37
つまりこの水溶液の濃さ(濃度)は約37%となります.
問5
まず,砂は水に溶けないという前提の下でこの問題を考えていきます.
いま,Aという物質がかなり多めにあったとしましょう. ここに水10gを加えたとき,Aが5g溶けたとします. さて,さらに同じ温度の水を10g加えるとAはどのくらい溶けるでしょうか.
答えはもちろん5gです。Aが溶けきらない限りは,同じ温度で同じ量の水を加えると決まった量ずつ溶けていきます.
仮に溶けた量が途中で少なくなったら,それはAが溶けきった証拠です. まだ水がAを溶かすことができるのに,Aが先になくなることでそのとき溶けたAの量が,溶ける最大の量よりも少ない量として出てきます.
今,問題で最初に水を加えたとき,溶け残ったのは32gでした. そして次に30gの水を加えて溶け残ったのは21.2gでした. これの差を計算すれば,水を加えたことで溶けた食塩の量が分かります.
30-21.2=8.8より,ここで8.8gの食塩が溶けたことになります(砂は水に溶けません).
そして問題ではさらに先ほどと同じ温度の水を,先ほどと同じ30gだけ加えて,そこで14gの溶け残りが出たと書いてあります.
これと21.2gの差を計算すると、21.2-14=7.2gより,7.2gの食塩が溶けたことになります.
この時点で食塩が溶けきってないとしたら,1回目に水を加えたときと同じだけの8.8gが溶けてないといけないので,最後に水を加えた時点で食塩は途中で溶けきってしまい,まだ水は食塩を溶かせる状態のままになったことが考えられます.
つまり,最後に溶け残った分の14gは全て砂ということになります.
したがって,50-14=36より,50gの中に混ざっていた食塩は36gです.
問6
ア:片栗粉は水に溶けません。
イ:コーヒーシュガーはお湯に溶けます。
ウ:氷をお湯に入れてかき混ぜたときに起きるのは,水に溶解するという意味の「溶ける」とは違い,氷から水になるという状態変化の「融解」という意味での「融ける(解ける)」です.
エ:水酸化ナトリウムは水に入れると溶けます.
オ:みそはお湯に溶けてはいません. その証拠に味噌汁は透明ではありませんし,時間が経つと味噌は下に沈みます. 水溶液になっているならば,それは透明で向こう側が見える状態であり,かつ時間が経っても溶けているものは全体に溶けたままで沈んでくることはありません.
問題2
解答2
- 問1 ア
- 問2 37.5%
- 問3 10g
- 問4 60℃
- 問5 50g
解説2
問1
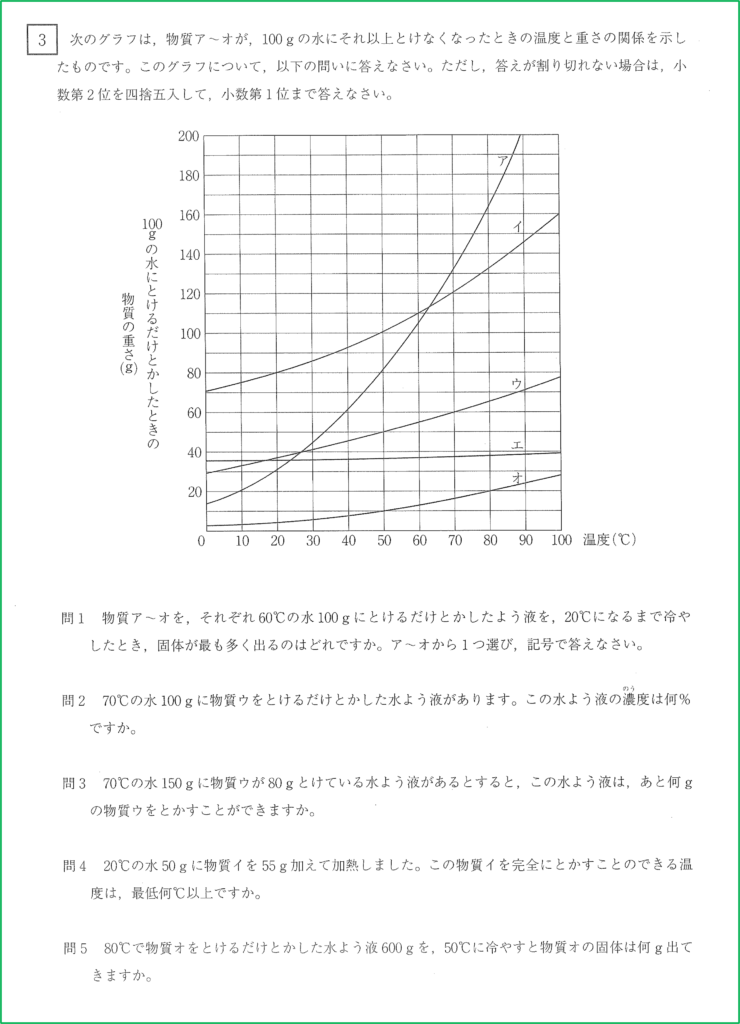
60℃の時の溶解度と,20℃の時の溶解度の差が大きいほど,その水溶液を60℃から20℃に冷やした時に出てくる固体の量が多くなるので,グラフの傾きが1番急な物質アが最も多く出てくると考えられます.
問2
溶解度の曲線のグラフより,物質ウは70℃の水100gに60gまで溶けることが分かります.
水溶液全体の重さに注意して計算すると,この水溶液の濃度は,
60÷(100+60)×100=37.5
よって,求める濃度は37.5%となります.
問3
同じ温度において,水の量が2倍,3倍,…になると,そこへ溶ける物質の重さも2倍,3倍,…となります.
今,問題では水が150gあり,これは100gの1.5倍です。つまりここに溶ける物質ウの重さは,70℃の水100gに溶ける限界の量の1.5倍の重さまで溶けることができます.
問2と同じようにして,物質ウは70℃の水100gに60gまで溶けることが分かるので,70℃の水150gに対して物質ウが溶ける限界の重さは,
60×1.5=90
よって70℃の水150gに対して物質ウは90gまで溶かすことができます.
今,問題では80gまで溶かしていると書いてあるので,
90-80=10
よって物質ウを残り10gまで溶かすことができます.
問4
水50gに物質イが溶ける限界の量が55gになる温度まで加熱すればよい.
グラフの情報が使えるようにするため,これを水100gのとき物質イが溶ける限界の量へと変換します.
水100gは,50gの2倍なので,物質イが溶ける限界の量も2倍になります.
55×2=110
よって水100gに対して物質イが110g溶ける温度が,水50gに対して物質イが55g溶ける温度と同じということです.
グラフより,水100gに対して物質イが溶ける限界の量が110gになるのは60℃であると読み取ることができるため,物質イを完全に溶かすためには最低60℃以上必要ということになります.
問5
物質オは80℃において,水100gに対して20gまで溶けます.
このとき水と物質オの重さの比は,水:物質オ=100:20=5:1です.
つまり水溶液全体の重さを6としたとき,そのうちの5が水で,1が物質オで占められているのです.
今,80℃において物質オを限界まで溶かした水溶液が全体で600gあるので,500gが水の重さで,100gが物質オの重さであることが分かります.
ここで50℃の水500gにおいて,物質オは最大何gまで溶けるか調べてみましょう.
グラフより,50℃の水100gにおいて,物質オは最大10gまで溶けます.
水500gは水100gの5倍なので,溶ける限界の量も100gの時の5倍であり,
10×5=50
よって50℃の水500gに対して物質オは最大50gまで溶けます.
今問題の80℃の水溶液には水が500g,物質オが100g溶けているので,上との差を計算すると,
100-50=50
つまり50gの物質オの個体が出てきます。
余談:料理で使うお酢(食酢)に含まれる酢酸の濃度
濃度に関連した話を少し紹介します.
皆さんは料理に使うお酢を知っていると思います. お酢には「酢酸」と呼ばれる酸性の物質が含まれているため,それが酸っぱい原因となっています.
さて,ここで料理に使うお酢,すなわち食酢の全体の重さのうち,「酢酸」という物質の重さが占める割合を予想してみてください. どのくらいだと思いますか.
実はお酢の中に3~5%しか酢酸は含まれていません. 意外と少ないのですね.
あれが全部酢酸だったと考えるとどれだけ酸っぱくなってしまうのでしょうか.そんなことを考えるのも面白いですね.
まとめ……の前に
『個別指導塾テスティー』の公式LINEにて、
『中学受験を9割成功に導く』メールマガジンを
毎週、完全無料で配信中✨
塾の活用の仕方・最適な勉強法・親として子供をどう教導するかの指針など 中学受験するお子様を持つ親御さんが知りたい知識を幅広くご紹介!!
↓↓詳細は以下をタップ↓↓

まとめ
今回は水溶液の濃度に関して学習しました。水溶液の濃度に関しては関連する物質の性質に関する理解、公式の暗記の2つが重要になってきますので、理解と暗記を平行して取り組んでいくようにしましょう!


















